上のグラフは、対応のあるデータを １次元散布図 で表した場合です。
「対応のある」という言い方は、日常ではあまりしませんが、統計学では、 対応のある検定 として、教科書に必ず書いてあるくらいの使われ方をしています。
対応のあるデータとしてわかりやすいのは、「前後のデータ」です。 同じものについて、何かの前と後のデータが対応しています。
対応のある検定 もそうですが、「対応のある」の場合、「対応のない」の方法ではわからないことが分析できるようになります。
二重測定 のデータでは、２つの測定器で同じものを測定することで、対応ができます。
サンプルごとの因果効果の分析 では、同じサンプルについて、 事実と反事実 の対応があります。
予測精度の判定 では、同じサンプルについて、予測値と実測値の対応があります。
上のグラフは、対応のあるデータを
１次元散布図
で表した場合です。
この方法の良いところは、対応が３つ以上あってもできます。
この方法の悪いところは、サンプルが多いと、線が交差したりして、グラフがごちゃごちゃしてくるところです。
上の１次元散布図の例と同じデータを、
２次元散布図
にしたのが下のグラフです。
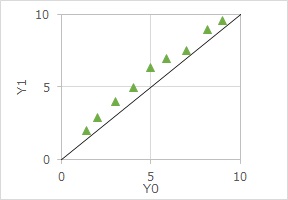
上の例では、原点(0,0)と、(10,10)を結ぶ直線も散布図に入れています。 このような線は、「斜め45度の線」と呼ばれます。（この呼び方を、どこの文献で見たのか忘れてしまいました。）
斜め45度の線は、対応のあるデータの分析では便利です。
例えば、この線よりも、全部のデータが上にある場合は、「全部のデータで、Y1の方がY0よりも大きい」という事を表しています。
二重測定 や 予測精度の判定 では、すべてのデータが、この線の上でばらつくような感じが理想的です。 この線の上にピッタリ乗ると、完璧です。
サンプルごとの因果効果の分析 では、データがこの線の上下でばらつく場合、「因果効果なし」や「因果関係なし」という考察になります。 この線の上側や下側に偏ると、「因果効果あり」や「因果関係あり」という考察になります。
２つの変数の差を調べたい時は、差をグラフにします。
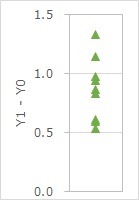
上のグラフは、差の値の、１次元散布図です。 対応のある検定 は、この値を検定の対象にしています。
１次元散布図では、「差はプラスの値に偏っている」といった事が調べられますが、２次元散布図の方が調べられることが多いです。
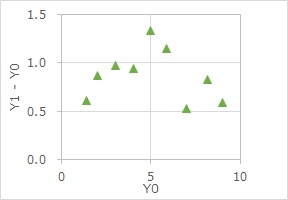
例えば、Y0に「基準」のような意味がある場合は、Y0を横軸にして、Y1-Y0を縦軸にします。
ARI因果効果モデル
では、このタイプを使っています。
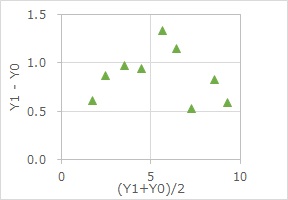
横軸をY1とY0の和や、平均値にすると、Y0にした時とは、違うことがわかることもあります。
（下の例では、Y0にした時と、特に変わらないですが。。。）
順路
次は
ネットワークグラフ
