サンプルごとの因果効果の分析

因果関係の分析では、因果効果で考えると、定量化によるメリットがあります。

サンプルごとの因果効果の分析には、さらにメリットがあります。

サンプルごとではない因果効果の分析

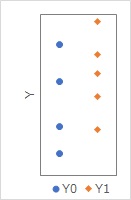
causal_effect
まず、上はサンプルごとではない因果効果の分析の例です。（対応のない）平均値の差の検定で分析した場合、「処置の効果はない」、という結論になるデータです。

下は、サンプルごとの因果効果の分析の例です。

上の例で、処置ありのサンプルについては、もしも処置をしなかった場合、処置なしのサンプルについては、もしも処置をした場合、という反事実のデータがあって、下のグラフになるとします。 Y0e、Y1eが、反事実のデータです。
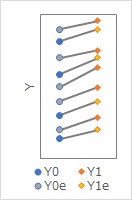
causal_effect

この例の場合は、全部のサンプルについて、処置ありの方がYが高いので、「処置の効果はある！」、という結論になって来ます。

サンプルごとのデータだと「効果あり」となるのは、各サンプルで基準になる値が違うためです。

この分析は、対応のある検定を使って、（対応のない）平均値の差の検定では検証できなかったことが検証できる事と似ています。

例えば、体質や購買量は、人によって違います。何かの処置（薬、キャンペーン、等）に効果があったかどうかを見るには、個人における処置の前後の差を分析対象にする必要があります。そのような分析が、対応のある分析になります。

因果効果の分析の例で、「もしも処置ありのサンプルが処置なしで、処置なしのサンプルが処置ありだったとしても、効果が同じようになるのかはわからない」と書きましたが、反事実のデータがあると、この懸念は考えなくて良くなります。

その意味で、疑似相関は排除できます。

ただし、同一人物の処置あり・なしのデータだとしても、処置ありが大人の時で、処置なしが子供の時のデータだとしたら、処置の効果なのか、大人と子供による違いなのかは、区別できないです。わかるのは、原因は特定できないけれども、Y1の時の方が高くなることだけです。

平均処置効果は、全体的な因果効果の分析の代表的なものです。

平均処置効果（Average Treatment Effect：ATE）というのは、サンプルごとの因果効果の平均値です。

処置ありと、処置なしの２つのグループの平均値の差ではなく、同じサンプルについて、処置ありと、処置なしの差を求めたものの、平均値です。