ネットワーク の理論は、いわゆる「ネットワーク」のようなものでなくても、当てはまります。
それぞれの分野には、特有の分析方法がありますが、比較的共通しているのが、 ネットワークを数字で表現する方法（書き方）と、絵で表現する方法（描き方）になります。 特に、絵については、これだけでネットワークの特徴がわかるので、 ネットワーク分析 の初歩であるだけでなく、とても重要なツールです。
数字による表現は、いろいろな視点での集計をする時に使います。
ネットワークグラフは、 ２次元散布図 で近くにあるもの同士を線で結んだグラフのようにも見えますが、違います。
２次元散布図を作るには、２点間の距離を、２次元の座標に変換する必要があります。
ネットワークグラフは、この座標変換ができないようなケース、例えば、「ＡとＢはとても近い。ＢとＣはとても近い。ＣとＡは、非常に遠い。」といったケースでも扱えます。 ネットワークグラフは、２次元の平面に描かれますが、意味があるのは、２点間を結ぶ線だけなので、 距離で考えると成立しない場合でも扱うことができます。
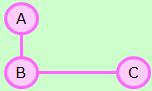
ネットワークの一番簡単なタイプは、辺と頂点の組み合わせだけで描かれています。
辺の長さや太さ、頂点の大きさに意味を持たせる場合もありますが、 それよりも、辺と頂点の結び付き方が注目される場合が多いようです。
例の場合は、AとB、BとCの間には、つながりがあります。 A、B、Cを頂点で表し、つながりを「辺」で表しています。
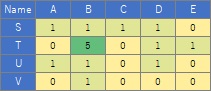
A、B、Cのネットワークを、数値で表現すると、下記の行列（表）の形になります。
この数値と絵は、見た目は違いますが、同じことを表現しています。
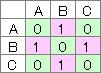
ちなみに、行列の対角線上の数値は、AからA、BからB、CからCのつながりを表しますが、例の場合は、つながりはないので、「０」になっています。 一般的に、対角線上が１になるネットワークは少ないですが、 例えば、コンピュータのハブの場合、一本のケーブルの両端を同じハブに接続すると、 「AからA」のような事が実際にできます。
簡単なモデルでは、例えば、AからBと、BからAには、違いを考えていません。 しかし、現実には、方向に意味がある事があります。 そのような場合は、矢印で表現します。 向きに意味があるグラフは、「有向グラフ」と呼ばれます。 意味がないグラフ（矢印を使わないグラフ）は、「無向グラフ」と呼ばれます。
また、数値の表現も、行列で０の場所が増えます。
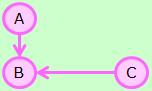
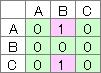
有向グラフは、 連関図 や ベイジアンネットワーク など、 因果関係 の分析（原因分析）でよく使います。
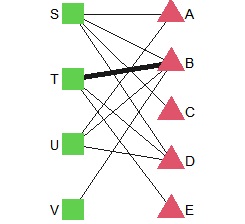
３つ目のタイプは、
２部グラフ
のデータです。
上２つは
A-A型
ですが、２部グラフは
A-B型
です。
Aの項目同士やBの項目同士には、矢印の有無に関わらず線は引かれません。
Rによる実施例は、 Rによるネットワークグラフ にまとまっています。
順路
次は
２部グラフ
