ネットワーク を科学的に扱うには、「どのようなネットワークなのか？」、といった事がスタートになります。 これがわかると、「ネットワーク上で何が起こるのか？」や、 「そのようなネットワークには、どうしたらなるのか？」といった事も調べられます。
このページは、「ネットワーク分析」というタイトルにしましたが、 正確に書くなら、「ネットワーク構造の分析」になります。
なお、一般的なネットワーク分析は、 A-A型の分析 の一種です。 A-B型の分析 の場合は、 Q分析 があります。
比較的新しいものとして、 グラフフーリエ変換とスペクトルグラフ理論 があります。
ネットワークの書き方と描き方 のページで、「一番簡単なタイプ」として、辺と頂点だけでできていて、辺に向きがなく、 辺の太さや頂点の大きさには意味を持たせていないタイプを説明しています。
とても簡単なモデルですが、このモデルで頂点や辺の数を増やしていくと、 現実のネットワークの特徴として知られている「スモールワールド」や、「スケールフリー」などの性質も説明できます。
このタイプの分析方法で面白いものとしては、 Q分析 があります。
頂点の数に対して、辺が多ければ、密度が高いネットワークと言えます。
一番簡単なタイプでは、辺の長さは考えません。 つながっていれば距離は「１」、つながっていなければ「０」になります。
A、B、Cが駅で、辺が電車のルートのようなものと考えると、 距離が１しかないのは不自然ですし、０は、あり得ない数字ですが、 情報の流れを扱ったりする時は、この表現でもうまく行っています。
例の絵の場合、AとCの間は、１＋１で、距離は２になります。
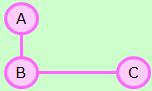
ネットワークが大きくなって来ると、ルートが複数ある場合が出て来ますが、 その場合は、最小値を距離とするのが一般的です。
ちなみに、簡単なモデルでは、「距離」と「ステップの数」を同じものとして扱う点でも、モデルが簡単になっています。
ひとつの頂点から出ている辺の数は、「次数」と呼ばれます。
例の場合では、AとCの次数は１で、Bは２です。
ネットワークが大きくなって来ると、様々な次数の頂点があります。 次数が特に多いと、「ハブ」と呼ばれます。
また、現実のネットワークの次数は、べき分布になっている事が多いそうです。 ネットワークの大きさに関わらず、べき分布になる性質は、「スケールフリー」と呼ばれています。
友達同士が友達であったりして、「世間は狭い」という経験をすることがありますが、 これは、「距離」で表現すると、「赤の他人への距離は、意外と短い事が多い」、とも言えます。
こうした現象は、「スモールワールド」と呼ばれています。
現実のネットワークは、複数の頂点がひとつの塊（クラスター）のように密接して関係している事があります。
これだけなら、赤の他人は遠いのですが、
塊のどこかから、別の塊のどこかに、ショートカットがあると、赤の他人への距離が、グンと縮まります。
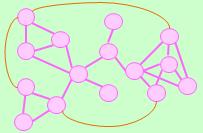
一番簡単なタイプから、辺と頂点を増やすことで、複雑なネットワークを表現できるようになります。 また、辺に向きを考えるタイプもあります。 これらとは別に、一番簡単なタイプの延長で、表現できることを増やす方法があります。
簡単なモデルでは、0と1だけで表現しましたが、 0と1以外の様々な大きさの数字を使うと、 つながりの強さも表現できるようになります。
つながりの強さを加味した場合、距離の近さと、つながりの強さの違いを、どのように区別するのかは、工夫がいります。
社会学では、ネットワークの辺の事を、「紐帯（ちゅうたい）」と呼びます。
例えば、同じ学校の生徒同士は、よく会いますが、 違う学校の生徒とは、つながりがあったとしても、会う事は少ない事が多いです。
このように、遠いクラスターとは、辺がつながっていても、つながりが弱い事があります。 これは、「弱い紐帯」と呼ばれます。
ネットワークの科学では、弱い紐帯に着目した分析や、応用が多いようです。 弱い紐帯からは、自分の属さないネットワークからの情報が入り、それは価値の高い情報になるそうです。
発言の量や、単語の使用回数など、 頂点の出現頻度に意味がある場合は、頂点の大きさ変える事で、それを表現する事があります。
例えば、都市の関係を上記のようなネットワーク分析の方法で研究する時は、 その都市の地図上の位置は、見ていません。
関係の強さの原因が、地図上の距離の近さだったとしても、原因の部分は見ていません。
地図上の関係も分析に入れたい場合は、距離もモデルの中に加えるか、あるいは、 パーコレーション で使われるような、格子のグラフにする方法があります。
ネットワークとしての性質よりも、空間の配置の性質が重要な時は、 空間統計学 の方が適しています。
また、関係の強さのデータは、強さを辺の太さではなく、長さで表現する方法も考えられます。 これに近い方法として、関係の強さを距離という尺度で見る方法には、 多次元尺度構成法 があります。
「ネットワーク分析 Rで学ぶデータサイエンス 8」 鈴木努 著 共立出版 2009
中心性や距離などのネットワークの尺度のいろいろなものの計算や、ネットワークのグラフの描き方について、
Rのsnaやigraphを使った計算方法が書いてあります。
二部グラフ（モードが２つ）の中心性や、
ベイジアンネットワーク
の作り方も出て来ます。
ベイジアンネットワークは、循環がないことや、因果関係のモデルな事が特徴のネットワーク。
「ネットワーク科学の道具箱 −つながりに隠れた現象をひもとく−」 林幸雄 編著 近代科学社 2007
スケールフリー性を中心にして、尺度、ツール、モデルといったものを紹介しています。
「Python言語によるビジネスアナリティクス実務家のための最適化・統計解析・機械学習」 久保幹雄 他 著 近代科学社 2016
グラフ、統計解析、機械学習、ネットワーク分析、最適化、Excelとの連携、といった事をするのに使うツールが、
Pythonではモジュールとしてまとまっているそうです。
この本は、モジュールの使い方事典のような内容です。
Pythonの本としては珍しく、ネットワーク分析にもかなりのページを割いています。
「マンガでわかる 複雑ネットワーク ： 巨大ネットワークがもつ法則を科学する」
右田正夫・今野紀雄 著 ソフトバンククリエイティブ 2011
左ページが文章で、右ページがマンガになっています。
対数の説明もされていて、親切設計な本です。
インターネットや、生態系のネットワークを同じように扱う理論として、複雑ネットワークを紹介しています。
生態系のネットワークを、食物連鎖のピラミッドのように考えてしまうと、
最上位や最下位の生物が重要な感じがします。
しかし、そうではなく、ハブの役目の生物が重要だそうです。
「ネットワーク科学 つながりが解き明かす世界のかたち」 Guido Caldarelli、Michele Catanzaro 著 丸善出版 2014
ネットワークは、社会でも自然でも、分野を問わずに表れる性質。
ネットワークの研究の初期は、単一のネットワークを扱っていたが、現在はネットワーク同士の関係性や、多重性が研究されるようになっている。
テキストのネットワークでは、共起で単語の意味が決まってくる。
ネットワークの形成は、自己組織化現象の一種。
現実のネットワークでは、辺で結ばれた頂点同士の次数には、正や負の相関がある。
この相関は、そのネットワークの形成にある自明ではないルールが原因。
「スモールワールド ネットワーク構造とダイナミックス」 ダンカン・ワッツ 著 栗原聡 他 訳 東京電気大学出版局 2006
スモールワールドの研究史があります。
「複雑ネットワーク入門」 今野紀雄・井出勇介 著 講談社サイエンティフィク 2008
ネットワークの数学的な基礎の解説書
「社会を<モデル>でみる 数理社会学への招待」 日本数理社会学会 監修 勁草書房 2004
「なぜ禁煙に失敗するのか」から始まり、「なぜ○×のか」、というタイトルの章が44個あります。
この疑問をテーマにして、それに合うモデルを解説するスタイルです。
（筆者には、この疑問文が本当にそうなのかの説明が必要のように思えましたが、、、）
22〜24章がネットワーク分析です。
22章：立場は同じでも、多くの人と会話する人は、権力をもつようになる。
23章：レギュラーネットワーク（近接する特定の人だけつながっている）を、ランダムネットワークに近付けて行くと、平均距離は、すぐに劇的に短くなるが、
クラスター性は、簡単には低くならない。
つまり、現実のネットワークでは、平均距離は短く、クラスター性が高い状況が起きやすいと言える。
これは、世界の狭さの証明になっている。
24章：弱い紐帯の理論は、強い弱いだけではなく、負（マイナス）の場合や、時間的な変化もモデルに取り入れると、現実に近くなる。
「ネットワーク分析 何が行為を決定するか」 安田雪 著 新曜社 1997
スモールワールドになる原因が解明された1998年から、ネットワーク分析が盛んになっていると言われているので、
「この本は、その前の時代の内容を知るのに良い本」、と思ってます。
この本で扱っているのは、産業、転職、夫婦などの関係。
「ネットワーキング論」は、ネットワークが形成される過程を対象にして、
ネットワーク分析は、できたネットワークを対象にする。
紐帯は、関係の強さの尺度。
紐帯には、交際頻度や、取引額などがあり、どれを選ぶのかで、ネットワークは違ってくる。
ネットワークのデータを取るための、アンケートの話もある。
「実践ネットワーク分析 ：関係を解く理論と技法」 安田雪 著 新曜社 2001
ネットワーク分析の指標や道具は、これまでの様々な研究から確立されてきた。
ネットワークを分析する研究と、ネットワークから分析する研究がある。後者が特に大事。
社会学では、「行為は、それを取り巻くもので決まってくる」、と考えるので、ネットワーク構造の把握が必要になる。
経済学では、「行為は、効用（利益）が最大なものが選ばれる」、と考える。
「Pajekを活用した社会ネットワーク分析」 ウオウター・デノーイ 他 著 東京電機大学出版局 2009
社会ネットワーク分析の３つのトピックは、凝集性、仲介、序列。
トピックによって、無向グラフと、有向グラフを使い分ける。
ネットワーク分析で見るものは、ネットワークの結合の仕方と、中心性。
ブロックモデリングは、ネットワークの図と扱う内容は同じだが、解析に便利。
社会心理学に、
バランス理論というものがあり、「正の紐帯はクラスタ内、負の紐帯はクラスタ間」としている。
この本は、Pajekという解析ソフトのマニュアルにもなっている。
Pajekには、ネットワークの時系列を扱う機能もある。
「社会の見方、測り方 計量社会学への招待」 数理社会学会 監修 勁草書房 2006
SEM、
クラスター分析などの、社会学の中での使い方が詳しく説明されている。
ブロックモデル：ブロックに分け、ブロックの関係を見ることで、全体像をわかりやすくしている。
ネットワーク分析としては、十数人の規模の、労働者の人間関係の分析があります。
「ネットワーク・ダイナミクス 社会ネットワークと合理的選択」 佐藤嘉倫、平松闊 編著 勁草書房 2005
ネットワーク分析と、合理的選択理論の融合についての本。
ネットワークの研究には、「ネットワーク（周囲の状況）で、行動が決まる」とする主張もあるが、この本は、
「ネットワークは、その人の行動の制約条件のひとつ」と考えている。
この本では、「合理的選択によって、ネットワークができる」というアプローチも出て来る。
ネットワークに変動を起こすのが、効用の最大化。
伝播のモデルでは、成員の特性、ネットワーク、環境の、どれを均質と仮定するのかで、モデルの性質が変わって来る。
「都市社会学・入門」 松本康 編 有斐閣 2014
都市の研究では、
ネットワークの構造が人々の意識や行動にどのように影響するのかや、
ネットワークがどのように形成されるかが注目されている。
親族、隣人、友人、出身コミュニティの関係の研究がある。
「社会ネットワーク分析の基礎 ：社会的関係資本論にむけて」 金光淳 著 勁草書房 2003
様々な分野への橋渡しも意識して、書かれています。
「テキストデータの統計科学入門 」 金明哲 著 岩波書店 2009
テキストマイニング
の本です。第６章がネットワーク分析になっています。
中心性などの、統計量の解説もありますが、この本が注目しているのは、ネットワークのグラフを描く技です。
Rの具体的な使い方も説明しています。
言葉の共起があれば、「つながりがある」と考えて、ネットワーク分析をしています。
この章の内容は、
https://www1.doshisha.ac.jp/~mjin/R/61/61.html
（著者ご本人のホームページ）に、ほぼ同じ内容があります。
「ビッグデータを活かす技術戦略としてのテキストマイニング」 菰田文男、那須川哲哉 編著 中央経済社 2014
第２章で、ネットワーク構造の時系列分析をしています。
５つの時期について、ネットワーク密度や、ネットワーク類似度を計算したり、ネットワーク構造図を描いてみて、変化を考察しています。
順路
次は
ネットワーク上の伝わり方
