（A1、A2、A3、A4）＝（2、2、1、2）
（B1、B2、B3）＝（2、3、2）
になります。
Q分析（Q-Analysis）は、 統計学 ではなく、幾何学（トポロジー）を基礎とする分析方法とのことです。
対象としているデータは、 行の項目と列の項目のそれぞれの交点について、関係があれば１、なければ０になっている表が元データになります。 次元数の分析や形の分析は、このデータだからこそ可能になっています。 値が０と１しかない A-B型 のデータです。
ちなみに、Q分析で使うような１と０の表のデータを、統計学的に分析する方法としては、 ISM があります。
Q分析は、 ネットワーク分析 に使うことができます。 特定の分野に限定される方法ではないてすが、 関係の構造を調べる方法として、 計量地理学 で使われていることが多いようです。
行の項目は横方向で、列の項目は縱方向で、１の数を数えます。
これが、それぞれの項目の次元になります。
図のデータで言えば、次元は、
（A1、A2、A3、A4）＝（2、2、1、2）
（B1、B2、B3）＝（2、3、2）
になります。
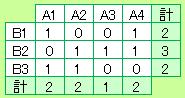
次元が近いほど、近いと考えます。 Q分析は、この次元の数で、行や列の項目を分類します。
このページの例では、次元数に大きな差が出ませんが、 項目数が増えると、差の大きさが何かを表していることがあります。 いろいろなものと関連を持っているものは、次元数が大きくなりますので、 都市の規模の分析等に使われています。
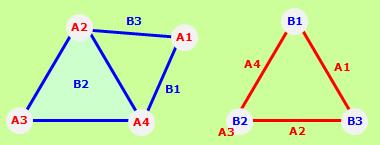
行の各項目について、その項目と1の関係になっている列の項目を、多面体や多角形の頂点と考えます。 頂点が同じ項目は、頂点を重ねることにすると、図形がくっついた図形ができます。
行と列を入れ替えて同様の手順をすると、頂点の項目が変わった図形ができます。
この図形で、データの表を視覚的に分析する事ができます。 面白いことに、この図形は、元のデータの情報を失っていません。 統計学では、元の情報が減って行きますので、だいぶ違う解析です。
ただ、今回の例は、最大でも3次元なので簡単に図形が描けるのですが、 次元が増えると、図形を描く方法が難問になります。
「地理空間分析」 杉浦芳夫 編 朝倉書店 2003
ひとつの章を割いて、Q分析を解説しています。
次元の解析方法として、隣接性・連結性・離心率と言った尺度を紹介しています。
空間データの解析方法が主体になっていて、
Q分析・
カオス
・
ニューラルネットワーク
、等が出て来ます。
「地域分析 データ入手・解析・評価」 村山祐司・駒木伸比古 著 古今書院 2013
数ページですが、「地域構造の明確化に役立つQ分析」という部分があります。
次元の小さい項目が、大きい項目に包含されるベン図を紹介しています。
「都市システムの時空間収束 MDSとQ分析の方法論的比較 行動計量学 33(2) 特集 地理学における多次元尺度構成法の応用」 水野勲 著 日本行動計量学会 2006
「時空間収束」というのは、交通や通信の発達で、都市間の時間的な距離が減少した現象のことです。
この論文では、MDS（
多次元尺度構成法
）とQ分析を比較しています。
MDSは一般に多次元データを二次元の平面上に縮約しますが、その際に失われるものがあります。
MDSは量的変化を扱うのに向いていて、Q分析は質的変化を扱うのに向いているそうです。
また、MDSは短期の変化の分析に向いていて、Q分析は長期の変化の分析に向いているそうです。
「特許情報のテキストマイニング 技術経営のパラダイム転換」 豊田裕貴・菰田文男 編著 ミネルヴァ書房 2011
テキストマイニング
の方法のひとつとして、Q分析が出て来ます。
第３章が「テキストマイニング結果の時系列変化とQ分析」になっています。
特許に出て来る単語の関連性を、Q分析で調べています。
いろいろな単語と関連性の高い単語は、次元が高くなります。
この本では、この分析を年毎にやってみて、次元の変化を見ています。
この解析のもうひとつ面白いところは、
いろいろな単語と関連している単語と、よく出て来る単語が必ずしも一致しない点です。
順路
次は
多対多対多の分析（A-B-C型の分析）
