A-B型の分析 では、Aという見方の要素と、Bという見方の要素の間の関係を分析します。
これの応用で、A、B、Cという３つの見方のそれぞれの要素の間の関係を分析する方法もあります。 さらに、この考え方は、４つ以上に増えても使えるようになります。
多対多の分析 の基本は、行列の形のデータと思います。 A-A型の分析 と A-B型の分析 はこのデータをスタートにすると考えやすいです。
テンソルを知っていると、「多対多対多はテンソルを使うのか？」となって来るかもしれませんが、 テンソルは数学的に複雑ですし、データを扱う時も手間がかかります。何より、データをイメージしにくいです。
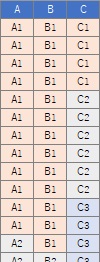
多対多対多の分析を一般化するのなら、テンソルの話になりますが、 ここではもっと限定されたケースになります。 ここで扱うデータは、質的変数が３つあるデータです。 このデータの場合は、多重対応分析が使えます。
なお、この量的変数が３つあって、それを多対多対多の分析をするのなら、テンソルの話になると思いますが、 量的変数があったり、質的変数と量的変数が混ざっている状況の場合は、 １次元クラスタリング を使うと、質的変数だけのデータに変換できるので、多重対応分析が使えます。
質的変数が３つあるデータについて、 対数線形分析 を使うと、これは３つの変数の関係の分析にはなりますが、 多対多対多の分析にはなりません。
質的変数が３つあるデータについて、 多対多対多の分析をする方法としては、 カテゴリの類似度の分析 が当てはまって来ます。
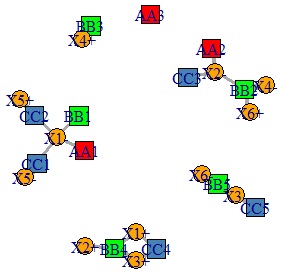
多重対応分析の手順は、２つの質的変数のあるデータをスタートにして、 コレスポンデンス分析 （対応分析）をする時と同じです。
多重対応分析をすると、個々のカテゴリの近さだけでなく、分析用に元のデータにはない変数が作られ、それとの関係で見ることができます。 カテゴリの類似度の分析 の多くでは、こうした変数は作られません。
Rによる実施例は、
Rによるコレスポンデンス分析
のページにあります。
順路
次は
テンソル
