重回帰分析 や パターン認識 は、一対多（Yが1つ、Xが複数）の分析方法です。 多対多の分析方法というものもあります。
多対多の分析では、複雑な関係を、できるだけシンプルに見る事を目指します。
多対多の分析には、いろいろなアプローチがあります。 このサイトでは、分析のスタートにするデータの型として、 A-A型の分析 と、 A-B型の分析 の２種類に大別してみました。
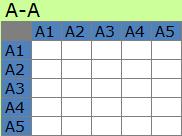
A-A型は、A1とA1以外、A2とA2以外、といったような関係を見ます。
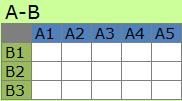
A-B型は、A1とBの項目全部、B1とAの項目全部、といったような関係を見ます。
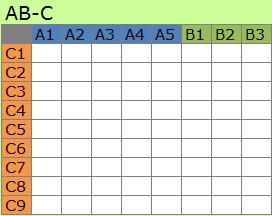
AB-C型は、A-B型の特別なものです。 異なるデータセットを行の項目をキーにして合体させた場合や、３つの列で分割表を作るとこの形（３元配置分割表）になります。
AB-C型の分析方法としては、
正準相関分析
があります。
多対多の分析が使われる場面として、前処理の有無があります。
前処理が無しというのは、A-A型やA-B型のデータが既にあるところがスタートになる場合です。
前処理が有りというのは、何らかの処理をして、A-A型やA-B型のデータを作ってから、多対多の分析になります。 変数の類似度の分析 や サンプルの類似度の分析 は、この処理をしています。 それぞれ、Aのところに、変数の項目名が来たり、サンプルの項目名が来るように前処理をします。
ミクロの分析というのは、「A1と関係が強いのは、どの項目か？」といった分析です。
マクロの分析というのは、A-B型だとできる分析ですが、「Aのグループと、Bのグループに関係があると言えるか？」という分析です。
多対多の分析に欠かせないのが、 ネットワークグラフ です。
行列形式のデータを直接的に見るグラフとしては、 ヒートマップ もありますが、ネットワークグラフの方がシンプルです。
これらの型の行と列の項目に何を持ってくるのかは、データ分析者の自由です。 データ分析者の腕の見せ所と言えるかもしれません。
それぞれの型には、どのような行列があるのか、その行列にするとどんな手法があるのか、どのようなグラフで表現できるのか、といったことを意識して、 データを変換すると、シンプルでわかりやすい結論を導けることがあります。
多対多の分析のデータは、 一対評価 で最初からこの型のデータを集めることもできますし、A-B型がスタートにあって、これをA-A型や異なるA-B型に変換して、この形に持ち込むこともあります。
順路
次は
A-A型の分析
