A-A型は、Aという見方について、要素間の1対1の関係を表しています。
多対多の分析
としては、一番シンプルです。
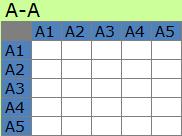
A-A型のデータの分類として、「対称行列・非対称行列」というのがあります。
対称行列は、対角成分を中心にした時に、左右対称になっている行列です。 例えば、(3,2)と(2,3)の値が同じになっています。
非対称行列は、対称行列の規則性がない行列です。
各要素の数字が「距離」（値が大きいほど関係が遠い事を表す）になっている、距離行列は対称行列です。
距離行列を分析のスタートにする方法には、 多次元尺度構成法 があります。
ネットワーク の分野で使われる「隣接行列」の内、項目のつながりの大きさだけを見ている場合は、対称行列を使います。 ネットワークのデータの場合、一番シンプルなのは、0と1で、各要素がつながるかどうかを表している形です。 0と1以外の数字も使う場合は、値が大きいほど関係が近い事を表しています。
ネットワークの書き方と描き方 では、矢印のある有向グラフを使います。
可到達行列は、隣接行列の一種です。 ISMとDEMATEL で使われています。
共分散行列や 相関行列 は対称行列です。
固有値解析 する方法があります。ちなみに、この方法は、 主成分分析 と同じです。
P(X|Y)とP(Y|X)のような条件付き確率を行列の形で集計すると、非対称行列です。
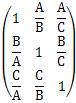
比や差による一対評価
は非対称です。
比や差による一対評価 のデータは、 固有値解析 をします。 この方法は、 AHP として知られています。
多次元尺度構成法 は、サンプルの類似度の分析の代表的なものですが、この方法は、元々、アンケートデータのように心理的な類似度のデータを分析する方法として、 開発されて来ています。
アンケート・感性評価 をする時は、２つのものを並べて、「どれくらい近いか？」という一対評価をした方が、答えやすいことがあるので、 人間のこうした性質を利用してデータを集めています。
A-A型は、データ分析の最初からA-A型になっているのではなく、テーブルデータの中間処理として、データ分析の計算の途中で、 元のデータをA-A型にする使い方があります。
ちなみに、データ分析のソフトでは、テーブルデータからスタートしても、A-A型からスタートしても、使えるようになっているものもあります。
変数の類似度の分析 では、変数の類似度の尺度を、例えば、相関係数にして、相関行列を作って行きます。
サンプルの類似度の分析 では、サンプルの類似度の尺度を、距離にして、距離行列を作って行きます。
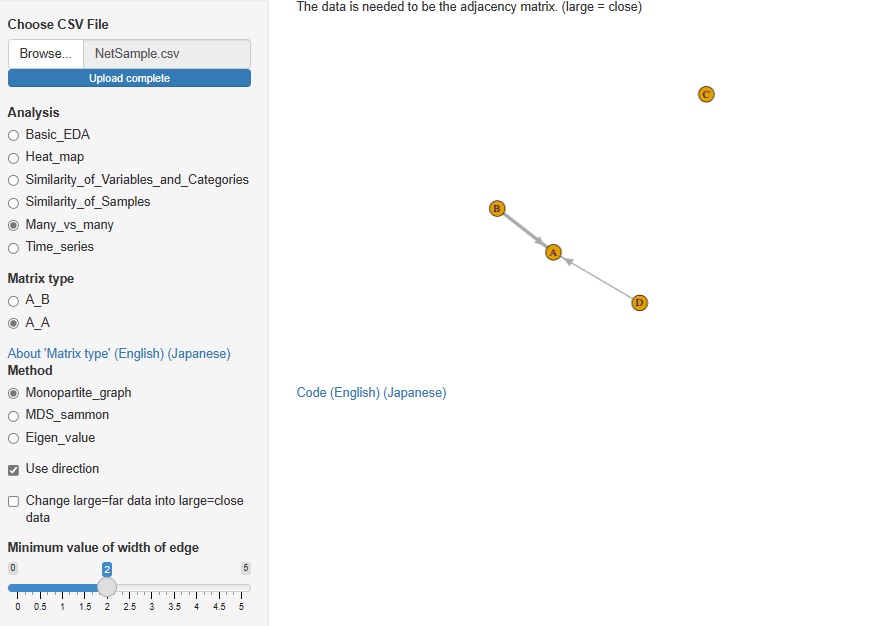
R-EDA1 では、A-A型の分析ができるようになっています。
隣接行列をスタートにした時のネットワークグラフによる分析、
距離行列をスタートにした時の多次元尺度構成法（MDS）による分析、
相関行列や一対評価のデータをスタートにした時の固有値、固有ベクトルによる分析ができるようにしてあります。
順路
次は
距離行列の分析
