距離行列の分析

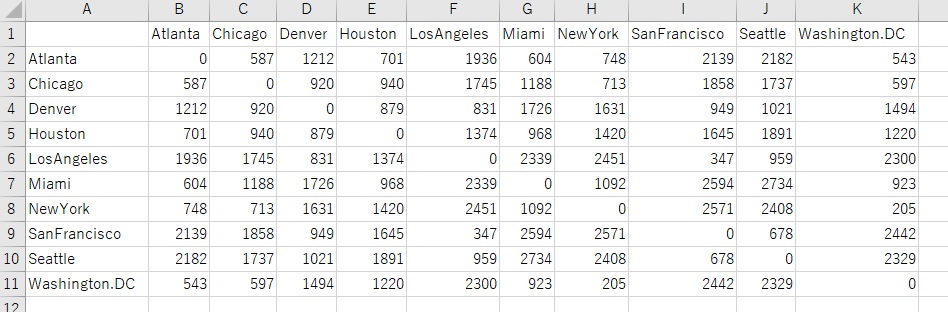
R-EDA1
距離行列というのは、成分が２点間の距離になっている行列です。例えば、上のデータは、米国の都市の距離を表しています。

グループ化による分析

クラスター分析は、距離行列について、項目同士の近さからグループを作って分類する方法です。

例えば、平面上の座標データがあれば、２点間の距離は、X方向の差、Y方向の差の、２乗和の平方根です。このように、座標データがあれば、２点間の距離を求めて、距離行列を作ることができます。

逆に、距離行列から座標データを求める方法が、多次元尺度構成法です。

例えば、10次元にある２点間の距離について、距離行列があり、それから座標データを求める場合は、10次元データとして求めると、元のデータの配置を正確に再現できます。

距離行列による次元圧縮は、10次元データから作った距離行列だとしても、何らかの情報は見ないことにして、２次元上の座標データとして求める方法です。

距離行列は、「近ければ近いほど、値が小さい」という性質のある行列です。

文字通りの「距離」のデータでなかったとしても、「近ければ近いほど、値が小さい」という性質があるデータなら、距離行列の分析方法は使えます。

また、例えば、相関行列は、「近ければ近いほど、絶対値が大きい」という性質ありますが、この場合何らかの変換をして、「近ければ近いほど、値が小さい」という性質になるようになれば、距離行列の分析方法は使えます。変数の類似度の分析では、相関行列や相関行列と似た性質の行列を扱いますが、この時に応用できます。

高次元を２次元に圧縮して可視化の方法は、高次元座標から作られる距離データから、低次元座標データを作ります。

この変換に無理がある場合の方法としては、変換はやめて、ネットワークグラフとしてデータを可視化する方法があります。

距離行列は、「２次元や３次元などの空間内にある点同士の距離」という想定があるデータです。そのため、距離から座標に変換できます。

空間データは、「ＡとＢは近い。ＢとＣは近い。だから、ＣとＡは近い。」というのが普通です。

ところで、例えば、空間データではないと、「ＡとＢは目が似ている。ＢとＣは口が似ている。ＣとＡは、似ているところがない。」という場合があります。この場合、座標データへの変換は無理があります。

ちなみに、これと似た話が、数量化Ⅵ類にもあります。

座標データに変換できないと、散布図での分析はできないです。

一方、ネットワークグラフは、距離行列を直接的にグラフにするだけで、上記の「だから、ＣとＡは近い。」に相当する想定が入らないです。このため、空間データではない場合の分析方法に向いています。

R-EDA1では、距離行列をスタートにして、クラスター分析や多次元尺度構成法ができるようになっています。
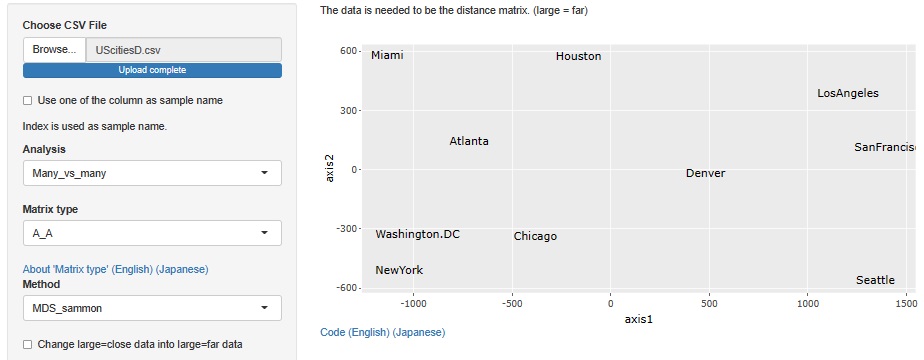
R-EDA1

R-EDA1では、「近ければ近いほど、値が大きい」という性質のデータの場合に、「近ければ近いほど、値が小さい」に変換する機能もあります。