距離行列の分析 の中でも、距離データを座標データに変換する方法は、 多次元尺度構成法 として、古くからあります。
Rを使った 多次元尺度構成法 の実施例になります。 下記は、コピーペーストで、そのまま使えます。 この例では、入力データは量的データになっていることを想定しています。 質的データがあるとエラーになります。
この例では、Cドライブの「Rtest」というフォルダに、
「Data1.csv」という名前でデータが入っている事を想定しています。
library(MASS)# ライブラリを読み込み
library(som) # ライブラリを読み込み
library(ggplot2) # パッケージの読み込み#
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data1 <- read.csv("Data1.csv", header=T) # データを読み込み
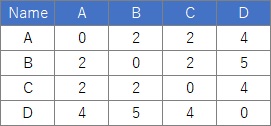
Data11 <- Data1[,2:5]# 距離データのある列を指定。この例は2から5列目の場合
Data11_dist <- as.matrix(Data11)# データを行列型に変換
sn <- sammon(Data11_dist) # 多次元尺度構成法
output <- sn$points# 多次元尺度構成法によって、得られた2次元データの抽出
Data <- cbind(output, Data1) # 元データと多次元尺度構成法の結果を合わせる。
ggplot(Data, aes(x=Data[,1], y=Data[,2],label=Name)) + geom_text() # Nameを使った言葉の散布図
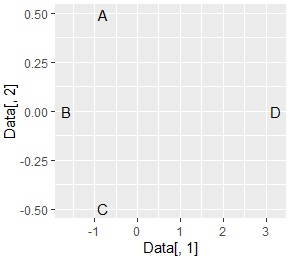
A、B、Cのグループと、D単独に分かれるはずで、だいたいそんな感じにはなりました。
Rによる高次元を２次元に圧縮して可視化 のページで、多次元尺度構成法は、距離行列を作ってから、距離行列を多次元尺度構成法の入力データとして使う流れになっています。 そのため、距離行列の形のデータを最初に持っている場合のやり方は、想像しやすいです。
多次元尺度構成法以外の方法でも、距離行列の形のデータから分析をスタートすることはできます。
また、アウトプットの次元数を２次元以外にすることもできます。 下記の例では、３次元にしています。
下記で、Data5ができれば、グラフの作成以降は、 Rによる高次元を２次元に圧縮して可視化 と同じです。
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T, row.names=1)
DM <- as.matrix(Data)
library(MASS)
sn <- sammon(DM, k = 3)
Data5 <- sn$points
library(Rtsne)
ts <- Rtsne(DM, perplexity = 3, dims = 3, is_distance = TRUE)
Data5 <- ts$Y
t-SNEの場合は、dimを４以上にすると、エラーになります。
library(Rcpp)
library(umap)
ump_out <- umap(DM,n_neighbors=5,input='dist', n_components = 3)
Data5 <- ump_out$layout
