量的変数が２つの時のデータ分析は、 相関係数 のページにあるような方法が基本です。 散布図を作り、相関係数を計算します。
このページは、量的変数が３つ以上ある場合です。
このページは、上にあるものほど、基本的な方法です。 下にいくほど、難易度が上がります。
２変数の時の方法を、たくさんの変数の組み合わせについて、片っ端からチェックする方法です。
相関係数 をすべての組合せについて計算して、表にまとめてものは、「相関行列」と呼ばれます。
相関行列は、 多変量解析 のいろいろな手法の中間的な計算で、よく使われています。
すべての組合せについて、散布図を作ったり、相関行列を作るツールは、様々なものがあります。
Rによる相関係数分析
のページだと、下図の方法を紹介しています。
これは、ひとつの表の中に、散布図と相関係数の両方が入っています。
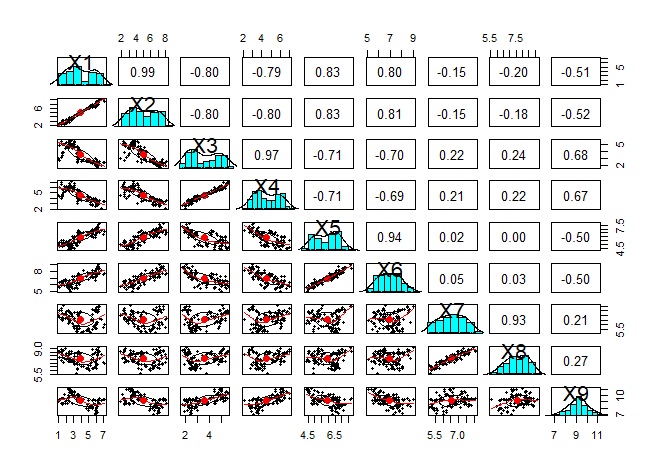
すべての組合せを調べる時に、XとY、YとXというように、二重に調べることになるのですが、このツールだと、ひとつの表に散布図と相関係数を入れることで、ダブりをなくしています。
偏相関係数 を勉強すると、「相関係数ではなく、偏相関係数を調べるのが、正しいのだ」という風に見えることがありますが、これは誤解です。
偏相関係数による分析 にあるように、相関係数と偏相関係数は、お互いを補完するような関係があるので、分析では両方使います。
相関行列には、負の値がありますが、それは正にして、ある値よりも小さい場合は0とみなす事にすれば、相関関係をネットワークのグラフで表現できるようになります。 相関行列で数字の羅列を眺めるよりも、グラフにした方がわかりやすい事があります。
こういったアプローチは、「グラフィカルモデリング」と呼ばれます。
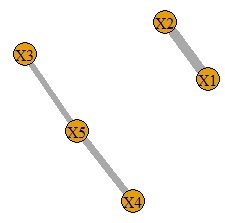
すべての組合せについて、相関係数や散布図を作って表形式にして見る方法は、変数が多くなって来ると、見にくくなってきます。 変数は、10個くらいが限度です。 それ以上では、ごちゃごちゃして分析が不可能だったり、処理するデータが多過ぎて、パソコンが対応しきれなくなったりします。
グラフィカルモデリングをすると、特に注目したいところが、はっきりと見えるようになります。
グラフィカルモデリングをしてから、気になるところを散布図で確認するようにすると、分析の見落としが減ります。
「グラフィカルモデリング」という名前で、偏相関係数をネットワークグラフにする分析方法が世の中にあります。 さらに、これに スパースモデリング を取り入れた グラフィカルラッソ という方法もあります。
相関関係の分析では、相関係数と偏相関係数の両方を調べた方が良いのですが、グラフィカルラッソでは相関係数についてはわからないことに注意が必要です。
変数の組合せを調べると、「XとY」、「YとX」というような組合せがありますが、相関係数や偏相関係数は、同じ数字になります。 ちなみに、散布図を作る時は、縦軸と横軸をどちらにするのかで見た目が変わりますが、回転すれば同じです。
そのため、相関係数や偏相関係数をベースにした分析では、無向グラフは作れても、有向グラフは作れません。
しかし、変数間に何らかの非対称があれば、有向グラフが作れます。
有向グラフになるデータの構造
のページにあるように、「何らかの非対称」というのは、いくつか種類があります。
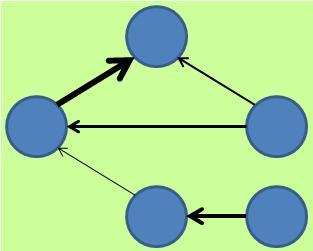
有向グラフが見つかると、「因果関係が、データから抽出できた！」や、もう少し控えめに、「因果関係の仮説が、データから抽出できた！」と思いたくなりますが、そうでもないです。
有向グラフになるデータの構造 にも書きましたが、非対称な構造と、因果関係は別の話です。
上記の方法は、質的変数でも似た方法があります。 質的変数用の、変数の類似度の分析 に書きましたが、質的変数の場合も知っていると、分析できることがさらに広がります。
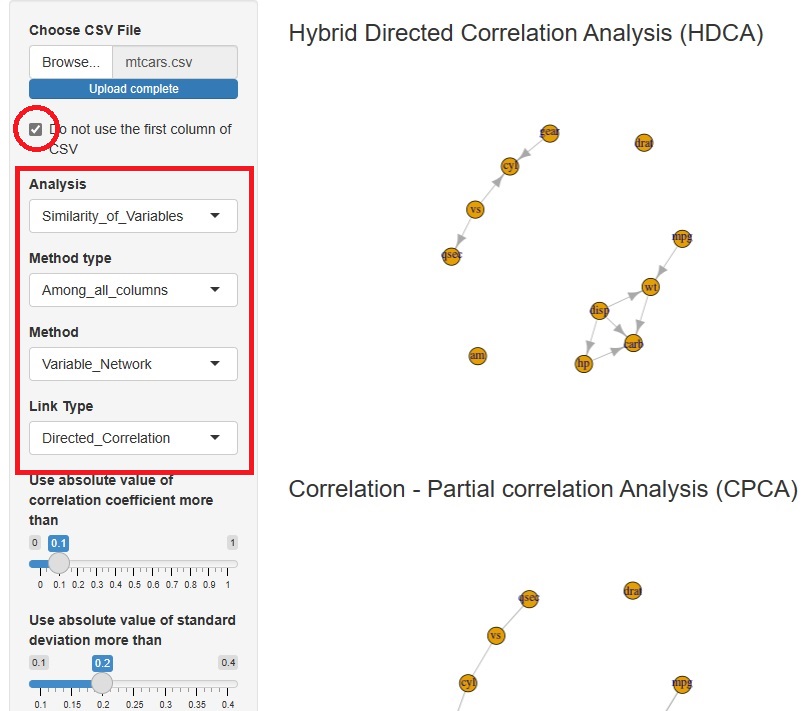
R-EDA1
では、データのcsvファイルを読み込んで、メニューを選ぶだけで、有向グラフによる相関分析もできるようになっています。
順路
次は
偏相関係数
