この例は、相関を調べたい変数が、X と Y で、その他に S と T という変数のデータがある場合です。
擬似相関 は、相関を調べる時に問題になることがあります。
偏相関係数は相関係数の一種です。 擬似相関を考慮することができます。
なお、偏相関係数は、 偏回帰係数 と名前が似ていますが、別物です。
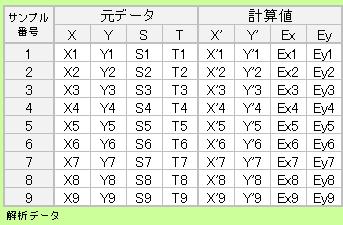
この例は、相関を調べたい変数が、X と Y で、その他に S と T という変数のデータがある場合です。
まず、
重回帰分析
で、
X' ＝ A × S ＋ B × T ＋ C
という式を求めます。
「'」は、予測値の意味です。
A、B、Cは偏回帰係数です。
例えば、データの１行目に、
X1、Y1、S1、T1
という数字があったすると、
X1' ＝ A × S1 ＋ B × T1 ＋ C
となりますので、１行目の予測値の X1' が計算できます。
もとのX1との関係は、
X1 ＝ X1' ＋ Ex1
となります。
Ex は、残差と言います。
変形すると、
Ex1 ＝ X1 − X1'
となって、Ex1 も計算できます。
X1' は、S1 と T1から計算されるので、「
Ex は、元の X から、S と T で説明できる部分を差し引いた値」、と解釈できます。
Y でも、 X の時の手順で、Ey が求まります。
準備はここまでです。
偏相関係数は、Ex と Ey の相関係数です。
具体的には、上記の手順で、（Ex2、Ey2）、（Ex3、Ey3）等も求まりますので、
これらのデータのセットから求まる相関係数です。
S と T が、X や Y にまったく関係のない変数の場合は、 A や B が、０に近い値になります。 そうなると、X と Y の相関係数と、Ex と Ey の相関係数は同じになります。
S と T 以外にも変数がある場合も、計算方法は、同様です。
複数の変数があり、i番目とj番目の変数の相関係数を、
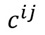
と表すとします。
このような相関係数を集めると相関係数行列ができます。
この相関係数行列の逆行列について、i番目とj番目の変数の組合せの成分を、
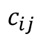
と表すとします。
すると、i番目とj番目の変数の偏相関係数は、以下で計算できます。
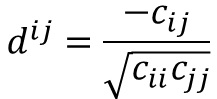
偏相関行列の一般的な計算では、上記の様にひとつずつ重回帰分析をしないで、相関行列の逆行列から求めるのですが、 この計算は、多重共線性がある組合せがあると計算できません。 例えば、２つの変数があり、各サンプルのそれらの変数の値が同じ場合は、このケースになります。
つまり、偏相関行列を調べる目的として、相関が高い組合せについての擬似相関を調べたい事がありますが、できないことがあります。 本末転倒しているので、偏相関行列による解析の最大の弱点だと思います。
この問題は、長い間ずっとあったのですが、 グラフィカルラッソ が解決策になって、偏相関行列を使って分析しようとしていたことができるようになりました。
擬似相関 の解析は、物理的な変数の意味がわからないと進まないです。 物理的な意味がわかっていると、偏相関係数で数値化することが役に立つのですが、 わかっていないと、解析の結果について解釈ができないです。 しかし、そもそも物理的な意味がわからなくて、この解析をすることが多いので、矛盾しています。
擬似相関が絡んでいる解析は、統計的なアプローチと、物理的なアプローチを、車の両輪のようにして進めるしかないと思います。 お互いのアイディアから、仮説とモデルを少しずつ組み立てて行きます。
偏相関行列の計算の弱点は、 物理的な意味がまったくわからずに、全変数の偏相関係数を網羅的に調べようとする時に問題になります。 少しでもわかっていれば、一部の変数だけ調べる等、工夫ができます。
名古屋大学 石井研究室の記事
相関係数行列から、偏相関係数行列を求める方法は、このページを参考にさせていただきました。
https://www.educa.nagoya-u.ac.jp/~ishii-h/materials/partial_correlation.pdf
順路
次は
グラフィカルラッソ
