上のようなデータがあったとします。 散布図を見ると、２つの変数の組合せは、どれもとても相関が高いです。 右側の数字が相関係数ですが、相関係数からも、相関が高いことがわかります。
「 擬似相関 を排除して分析したいから、 偏相関係数 で分析」とすると、おかしな事が起きます。
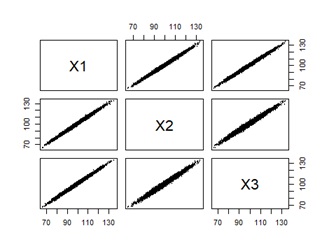
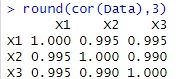
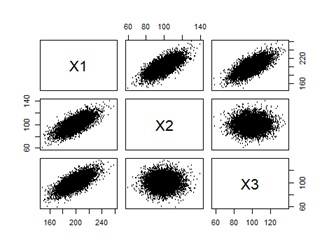
上のようなデータがあったとします。
散布図を見ると、２つの変数の組合せは、どれもとても相関が高いです。
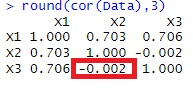
右側の数字が相関係数ですが、相関係数からも、相関が高いことがわかります。
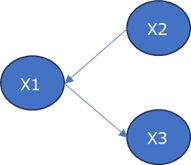
このデータは、下記のような構造でできています。
この絵の意味は、「X1に誤差が加わって、X2やX3ができている。X2とX3に加わる誤差は無関係」というものです。
つまり、X2とX3は
擬似相関
です。
上のデータの偏相関係数が下になります。
X2とX3の偏相関係数はとても小さく計算されました。
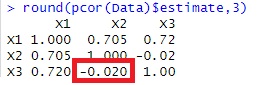
疑似相関がある場合に、偏相関係数を計算すると、疑似相関を見破れます。
上の例では、X1に誤差が足されて、X2やX3ができている場合に、相関係数ではわからないけれども、偏相関係数なら、その構造がわかる、としています。
下のように、X2に誤差が足されて、X1ができ、X1に誤差が足されて、X3ができている場合も、相関係数と偏相関係数は、同じような出方をします。
つまり、偏相関係数では、どちらに誤差が足されたのかが、わかる訳ではないです。
上のようなデータがあったとします。
散布図を見ると、X2とX3２つの変数の組合せは、相関がないです。
X1とX2、X1とX3については、相関があります。
相関係数からも、その関係がわかります。
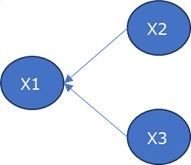
このデータは、下記のような構造でできています。
この絵の示すことは、例えば、「X1 = X2 + X3 + 誤差」ということを表しています。
因果関係の分析では、「X1 = X2 + X3 + 誤差」であることが特定できると良いのですが、
偏相関係数では、「X1 + 誤差 = X2 + X3」の可能性も否定できません。
上のデータの偏相関係数が下になります。
X2とX3の偏相関係数はとても大きく計算されました。
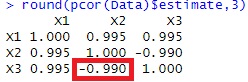
偏相関係数のこの性質は、X1という変数が入ると、X2とX3が独立しないこと、 つまり、条件付き独立は成り立っていないことを示しています。
筆者の場合、 「相関係数よりも、偏相関係数の方が、上位の評価指標」という誤解をしていたので、本来、「無関係なはずの変数間に、なぜ、関係があることになるのか？」となってしまって、困った経験があります。
上の例から、「変数の関係を調べる時は、相関係数と偏相関係数の結果から総合的に考える」という分析の仕方が良いことがわかります。
相関係数と偏相関係数を見比べる分析は、「この部分がこうなって、、、」と、ややこしい検討になります。
この後の分析の方向性として、筆者は２つ考えています。
ひとつは、向きがわかることを利用する方向性です。 偏相関係数による有向相関分析 が、その方法になります。
もうひとつは、向きにはこだわらず、 同じ変数間の相関係数と偏相関係数では、絶対値が小さい方が、知りたい情報になっている性質を利用する方向性です。 相関偏相関分析 が、その方法になります。
「グラフィカルモデリング」 宮川雅巳 著 朝倉書店 1997
偏相関係数と条件付き独立について、詳しく書かれています。
順路
次は
偏相関係数による有向相関分析
