トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

条件付き独立になるデータの構造

独立性の検定 をして変数の関係を分析をすると、 相関関係の探索 はできますが、データの構造の非対称性はわかりません。

条件付き独立による探索 をすると、 有向グラフになるデータの構造 が出せるようになります。

矢印は、因果関係を表さない

下の散布図は、３変数のデータの関係を表しています。

このデータは、AB = A + Bとなっています。

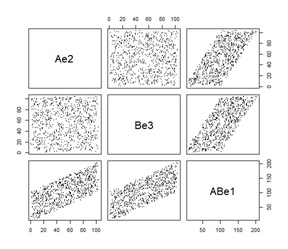
AB、A、Bの間に、もしも原因と結果の関係があるのなら、例えば、以下のようなものが考えられます。

• 「AとBが合わさって、ABができる」：AとBが原因、ABが結果
• 「ABからAが分かれ、残りがBになる」：ABとAが原因、Bが結果
• 「ABが分裂して、AとBができる」：ABが原因、AとBが結果

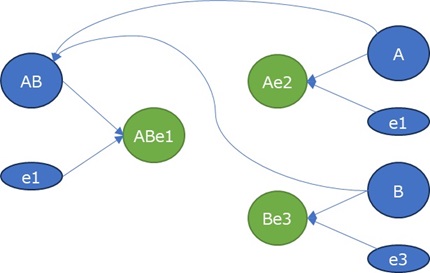
条件付き独立による探索 をすると、下のような有向グラフが描けます。 矢印は、AとBのそれぞれからABにつながっています。

この矢印が、因果関係を表すのは、「AとBが合わさって、ABができる」が、データの背景にある場合です。 「ABからAが分かれ、残りがBになる」と「ABが分裂して、AとBができる」の場合とは、矢印が一致しません。

つまり、条件付き独立を調べて有向グラフを作れたとしても、必ずしも因果関係を表していないです。

他の構造の場合

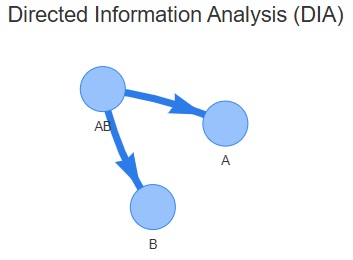
有向グラフになるデータの構造 は、他にもありますが、矢印と因果関係が必ずしも一致しないのは、同様です。 例えば、 有向情報量分析 では、下のようになります。 この場合は、「ABが分裂して、AとBができる」と矢印が一致しています。

順路 次は 回帰モデルになるデータの構造

杉原データサイエンス事務所によるコンサルティングとセミナー