条件付き独立による探索

独立性の検定をして変数の関係を分析をすると、相関関係の探索はできますが、データの構造の非対称性はわかりません。

「条件付き独立」について調べると、有向グラフになるデータの構造が出せるようになります。

条件付きの独立と、有向グラフの関係（質的変数）

AとBという質的データの変数が独立している場合、例えば、分割表は、下のようになります。度数にあまり偏りがありません。

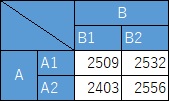
AとBという質的データの変数が独立していて、 AとBが条件付きでも独立している場合は、例えば下図になります。この場合は、度数にあまり偏りがありません。

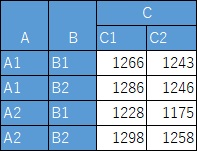
AとBという質的データの変数が独立していて、 AとBが条件付きでは独立しない場合は、例えば下の２つの例になります。この場合は、度数が偏っています。

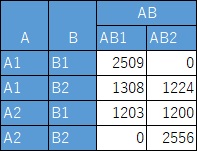
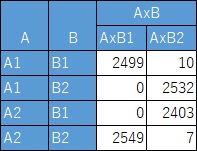
条件付きでは独立しない場合、有向グラフは下図になります。 AとBという変数同士は独立しているので、AとBの間には線がありません。

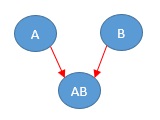
上記の考え方は、量的変数にも応用できます。

２つの変数を見ているだけだと独立なのに、第３の変数も加えると、独立していないように見える性質は、偏相関係数による分析で調べられます。

ベイジアンネットワークによるデータの構造解析にも書きましたが、変数がたくさんある時に、条件付き独立の関係を探索的に調べて、有向グラフを作る方法は、ボトムアップのアプローチです。

まず、２変数同士の独立性を調べて、独立の有無を調べます。

次に、３変数以上について、条件付き独立を調べて、２変数の調査では、「独立していない」となっていないとなった部分を切るかどうかを決めます。合わせて、わかる範囲で矢印の方向も調べます。

条件付き独立になるデータの構造には、因果関係に条件付き独立を使う場合の考え方をまとめています。

「つくりながら学ぶ！　Pythonによる因果分析　因果推論・因果探索の実践入門」　小川雄太郎　著　マイナビ出版　2020
条件付き独立だと、有向グラフは１通りに決まる説明があります。