回帰モデルになるデータの構造

重回帰分析の数理モデルの一番簡単な形は、
Y = X + e
という式です。

この式の意味は、「原因であるXに誤差が加わったものが、Yになっている」というものです。「Xに誤差が加わることで、Yができる」と解釈すれば、Xが原因で、Yが結果を表すモデルになります。

「誤差」があるという点や、それが「加わる」というメカニズムになっている点が当てはまる現象であれば、このモデルが、因果関係を表すモデルになって来ます。

Y = X + eの構造を、データから抽出する方法

現実のデータでは、YとXの両方の測定についても誤差が入って来ることが普通です。しかし、そういった誤差の影響が小さい場合は、 LiNGAM や、正規化による有向相関分析を使うと、
Y = X + e
の関係式をキレイに出せることがあります。

LiNGAM は、回帰モデルになるデータの構造の時に、有向グラフになるデータの構造を導いて、定量的な仮説の探索をする方法になります。

Y = X + e
の式がうまく出せる場合と、そうでない場合を整理しておくと、分析の参考になりますので、下記に整理してみました。

Xが操作できる量で、Yがその結果になっている場合は、Y = X + eが当てはまる可能性があります。

例えば、科目ごとに異なる試験時間がXで、クラスごとの実際の試験時間がYの時です。この場合は、実際に因果関係がありますし、このモデルが当てはまるはずです。

この後の話の逆になるのですが、Xのデータが真の値（誤差が０）でしたら、Y = X + eが当てはまる可能性があります。

「Y = X + e」という因果関係の仮説があるとします。直近の３か月間のデータを確認したところ、確かにそうだったとします。

こうなって来ると、「仮説が検証できた」と思いたくなります。しかし、例えば工場では、もう少し過去のデータを見ると、この式が当てはまらなかったりします。

この例では、時期によって関係性に違いがあることに、因果関係を解明するヒントがあったりします。シンプルな数式で表せるような因果関係ではないです。

この例は、時間的な偏りですが、空間的な偏りのこともあります。

因果関係があっても、式が当てはまらない場合があります。下のグラフの場合は、Xの、ある値を境にして、Yの値が決まっている場合です。
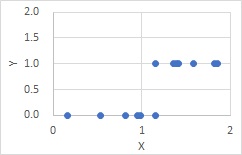
層別のグラフ

XもYも測定値の場合は、両方に誤差があります。

仮に、真の値同士には、
y = x
という関係があったとしても、持っているデータがXとYで、
Y = y + ey
X = x + ex
といったようになっているとすると、
Y = X + e
がモデル式ではないです。

「そうは言っても、
Y = X - ex + ey
にはなるから、実質的に
Y = X + e
になるのでは？」と考えたくなりますが、回帰分析の方法で、Xの係数が「１」であることを求めることはできず、「１」よりも小さな値が求まります。この話は、回帰分析への測定誤差の影響に詳しく書いています。