 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
YとXという2つの変数があったとします。 この時、「Y = X + eと、X = Y + eの、どちらなのか?」ということを、データから推定するのが、正規化による有向相関分析です。 (Normalized Directed Correlation Analysis : NDCA)
正規化(Normalization)は、 元のデータから最小値(Minimum:Min)を引き、それを範囲(レンジ:Range)で割ります。 範囲というのは、最大値(Maximamum:Max)と最小値の差です。
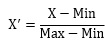
正規化されると、数字が0から1の間になります。
XとYのそれぞれを正規化すると、どんなデータでも、データが左下を原点(0,0)にした、縦横が1の正方形の中に収まる形になります。
「Y = X + eと、X = Y + eの、どちらなのか?」は、以下のように進めます。
上記で標準偏差としている部分を、回帰分析の傾きにしてもできます。
正規化と似たもので、標準化があります。標準偏差が1になるので、標準偏差を比べることができません。
一様分布の場合がわかりやすいので、一様分布を例にします。
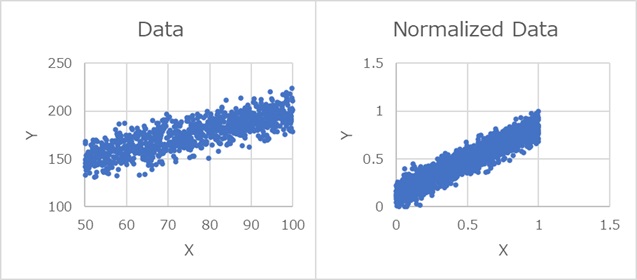
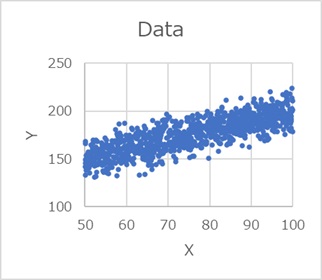
回帰分析のモデルの簡単なものは、「Y = a * X + b + e」という構造でできているデータを、正規化して、 Yを縦軸にしたのが、下の左の図です。Xを縦軸にしたのが右の図です。 Xとeは、それぞれ一様分布です。
左下のヒストグラムは、Xのヒストグラムです。 Xは、一様分布なので、ヒストグラムでも一様分布な様子がわかります。
右下のヒストグラムは、Yのヒストグラムです。 一様分布をしているXに、eの分が足されるので、分布の端の方が少なくなり、中心側が多くなります。 そして、分布は0から1の間に収まるようにするので、正規化したXの分布と比べると、端のサンプルが、中心側に寄る形になります。 この違いがあるので、Yの標準偏差の方が小さくなります。
そのため、Xの標準偏差とYの標準偏差の比が1より大きいかどうかで、構造がわかります。
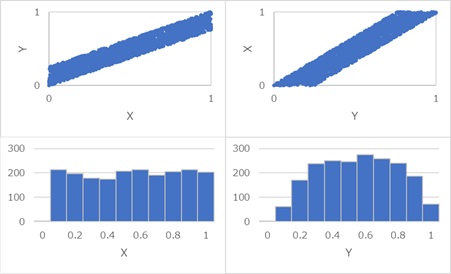
上記の法則は、Xの分布が一様分布のようになっていると、確実に成り立ちます。
正規分布のように、分布の端の方が少ない場合は、上記で使っている法則が当てはまらないです。
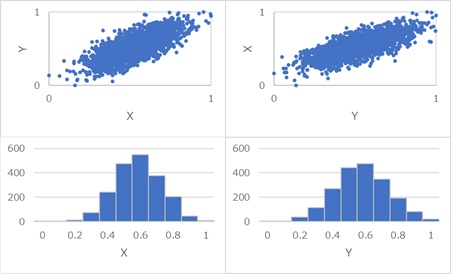
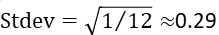
範囲が1の一様分布では、標準偏差が約0.29です。(「一様分布 分散」で文献が調べられます。上記の式の「12」という数字も出て来ます。)
構造が特定できる時の法則が成り立っているかどうかの確認をしないと、XとYの標準偏差の比で、構造が特定できないです。 筆者は、法則が成り立っているかどうかの目安としては、標準偏差の大きい方が0.29に対して、どのくらいなのかを確認すれば良いように考えています。 例えば、「0.2よりも大きければ、法則が成り立っていると考える」とします。
例えば、Xが正規分布のデータが正規化されると、標準偏差は約0.13になりますので、法則が成り立っていない可能性が非常に高いです。
左がデータ、右が
Rによる正規化による有向相関分析
による実施例です。
有向グラフが、うまくできています。
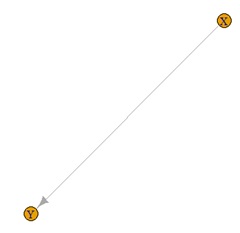
Rによる正規化による有向相関分析
を下の左の構造のデータに適用すると、右の結果になります。
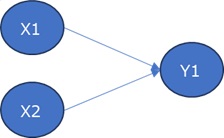
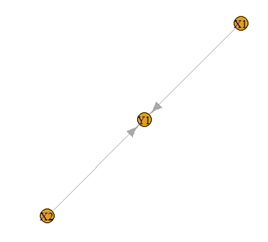
また、下の左の構造のデータに適用すると、右の結果になります。
X2を起点とする矢印の向きが特定できています。
この点は、
偏相関係数による有向相関分析
よりも優れています。
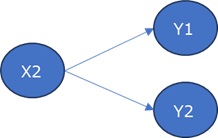
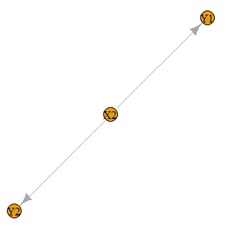
3変数以上でも構造が特定できる理由の考え方は、基本的に2変数の時と同じです。
まず、矢の元がひとつの変数の場合は、2変数の時と考え方が同じです。
Y1とX2、Y2とX2というそれぞれについて、2変数の時の考え方を当てはめます。

まず、矢の先がひとつの変数の場合も、構造の特定の仕方は、2変数の時と同じです。
Y1とX1、Y1とX2というそれぞれについて、2変数の時のように、標準偏差の比を計算して特定します。
Y1とX1の間で、構造を調べている時は、X2は誤差と同じ位置付けになります。

ハイブリッド有向相関分析 は、 偏相関係数による有向相関分析 と合わせることで、向きが特定できないケースを少なくするようにしています。
Rによる正規化による有向相関分析 に、上記の実施例のコードがあります。
順路


 次は
重回帰分析
次は
重回帰分析

