多変量データの相関分析 で分析できるのは、変数間の無向な関係です。 相関の高い・低いはわかりますが、変数間の向きはわかりません。
一方、 偏相関係数による分析 のページで、相関係数と偏相関係数でわかることが違い、また、向きによってその違いが表れていることがわかります。
このページの「有向相関分析」というのは、 偏相関係数による分析 をヒントにして、筆者が考えた分析方法です。 もしかしたら、 ベイジアンネットワークによるデータの構造解析 として、同じ方法がすでに世の中にあるかもしれないのですが、筆者の知る限りではないようです。 ご存知の方は、ご教示いただけると幸いです。
偏相関係数による分析 のページを改めて見ます。
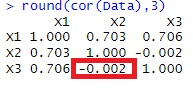
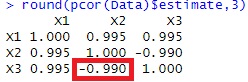
まず、X1が矢印の元の場合や、中間の場合、相関係数と偏相関係数を比べると、X2とX3は、X1を共通にしていることを表しているのは、偏相関係数の方です。
また、偏相関係数の方が絶対値が小さいです。
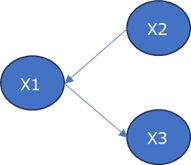
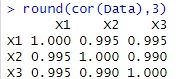
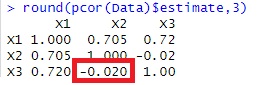
一方、X1が矢印の先の場合、相関係数と偏相関係数を比べると、X2とX3が無関係なことを表しているのは、相関係数の方です。
また、相関係数の方が絶対値が小さいです。
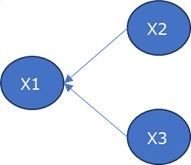
ネットワークグラフ の描き方のルールと、矢印の方向を合わせるのが、方針になりそうなことがわかります。
上記の方法は、矢印の中間、元、先にある変数が１個しかない構造の時に、うまく働きます。 複数あることは想定していません。
複数ある場合への対策は、 有向相関偏相関分析 になります。
出力の行列は、上から順に、相関係数の２乗、偏相関係数の２乗、グラフを描くためのデータです。 数字と、矢印の太さが対応しています。
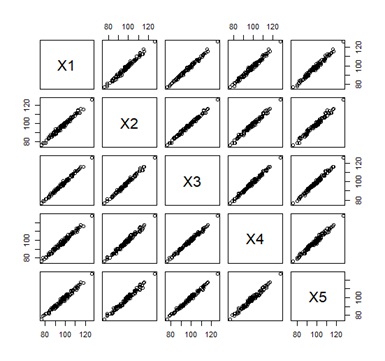
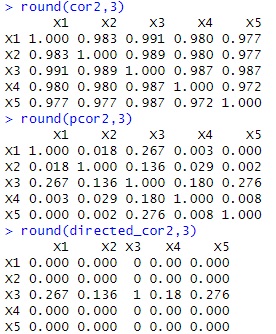
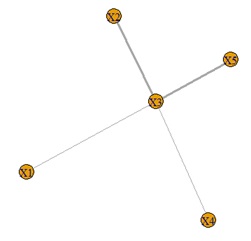
元か中間かは、区別できないため、無向グラフです。
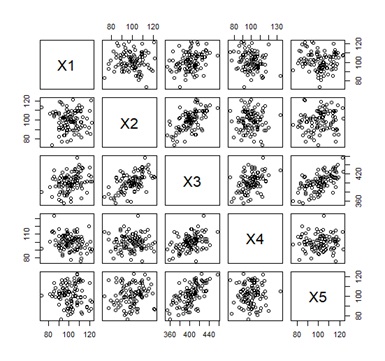
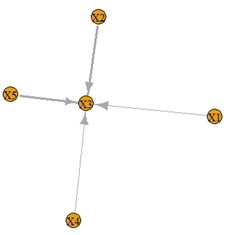
ベイジアンネットワークによるデータの構造解析 として、世の中では、以前から量的変数から有向グラフを導く方法が考案されています。
条件付き独立かどうか、つまり、偏相関係数からわかる構造を見て、矢印の向きを決めているようです。
このページのように、相関係数と偏相関係数の両方を見る方法は、筆者は見かけたことがないです。
Rによる有向相関分析 に、上記の実施例のコードがあります。
順路
次は
多重有向相関分析
