 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
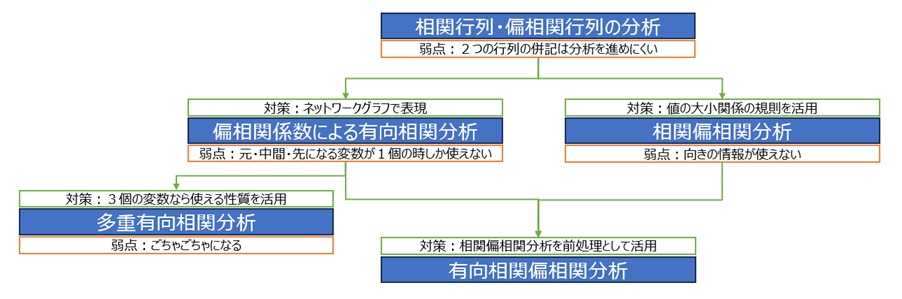
偏相関係数による分析
から、
偏相関係数による有向相関分析
、
多重有向相関分析
、
相関偏相関分析
といった展開があるのですが、いずれも弱点があります。
このページの有効相関偏相関係数による分析というのは、上記の方法の長所・短所を踏まえ、筆者が考案した方法です。
もしかしたら、同じ方法がすでに世の中にあるかもしれないのですが、筆者の知る限りではないようです。 ご存知の方は、ご教示いただけると幸いです。
偏相関係数による有向相関分析 には、元、中間、先に当たる変数が1個の場合に、面白い結果が出る方法です。 それ以外の構造のデータに使うと、訳のわからない結果になります。
「それ以外の構造のデータ」へのアプローチとして、「3つの変数の組なら、有向相関分析が使える」という知識を使って、 3つの変数の組み合わせを網羅的に調べ、結果を合成するのが、 多重有向相関分析 ですが、この方法では、うまく行きません。
一方、向きが出てくる面白さは諦めるものの、相関係数と、偏相関係数の両方を調べることによるメリットだけを効率良く進めるのが、 相関偏相関分析 です。
有向相関偏相関分析は、相関偏相関分析の結果は、調べるべき変数の組合せが特定できることに着目して、 多重有向相関分析のように、網羅的に調べることを回避します。


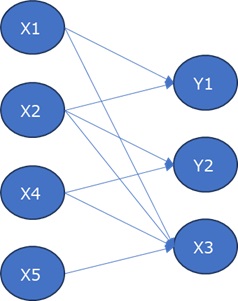
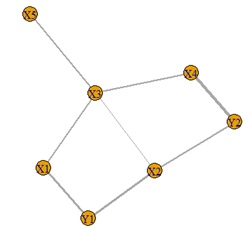
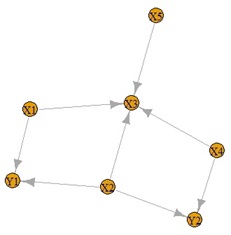
上のグラフから、左から順に、元データの構造、相関偏相関分析、有向相関偏相関分析です。
元データの構造を導き出せているので、なかなか良い方法のようです。
有向相関偏相関分析に限らず、 偏相関係数による有向相関分析 でも同じなのですが、「向き」として見ているのは、3変数以上があった時の条件付き独立の関係です。 上記の例では、例えば、 X1とX2は独立していて、Y1にX1とX2の両方の情報が入っている場合を見つける方法です。
どんなに相関が高いとしても、2変数しかない場合は、「向き」は見つかりませんし、そもそも分析対象でもなくなっているので、 因果関係の分析などで、この方法を使う時は、この点を前提とした使い方になります。
また、X1とX2が独立していないと、上記の例のような結果は、うまく出て来ない可能性もあります。
相関偏相関分析は、2変数の関係も消えないので、併用した方が良いです。 相関分析偏相関分析は、有向相関偏相関分析の前処理としての使い道だけでなく、この使い道もあります。
Rによる有向相関偏相関分析 に、上記の実施例のコードがあります。
順路


 次は
ハイブリッド有向相関分析
次は
ハイブリッド有向相関分析

