Y = X + e
is the simplest formula of
Regression Analysis
The meaning of this formula is that "Y is the cause of X plus an error."
It's a formula that is used as a matter of course, but in practice, problems occur. This page has been considered by the author through such troubles.
In real-world data, it is common for both Y and X measurements to be inaccurate.
However,
if the effect of such an error is small, you may be able to use LiNGAM
to get a clean
Y = X + e
relational expression.
LiNGAM is a method for Quantity Way of Making Hypothesis by deriving the Structure of data that becomes a directed graph when the structure of data that becomes a regression model .
If X is the amount you can manipulate and Y is the result, then Y = X + e may be true.
For example, when the exam time is different for each subject, X, and the actual exam time for each class is Y. In this case, there is a real causal relationship and this model should apply.
To the contrary of the following story, if the data of X is a true value (error is 0), Y = X + e may be applicable.
If you look at the data from the last three months, you find there are "Y = X + e".
However, in a factory, for example, if you look at a little more historical data, this expression may not apply.
In this example, there are hints to elucidate the causal relationship that there are differences in relationships depending on the time of year. It is not a causal relationship as expressed by a simple formula.
This example is a time bias, but it can also be spatial.
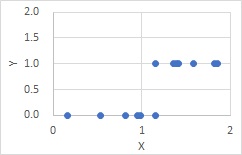
Even if there is a causal relationship, the formula may not apply. In the case of the graph below, the value of Y is determined with a certain value of X as the boundary.
I wrote something similar to the effect of measurement error on regression analysis, but if both X and Y are measurements, there is an error in both.
Even if there is a relationship between true values,
y = x
, if the data we have is X and Y, then
Y = y + ey
X = x + ex
The regression analysis method doesn't ask for the coefficient for X to be "1", but it asks for a value less than "1". This story is about the effect of Measurement Errors in Regression Analysis.
NEXT 
Proportional variance model data structure
