X1 = a1 * X2 + e1
X3 = a2 * X1 + a3 * X4 + e2
to calculate values of a1, a2, and a3, and to verify the goodness of the data to this model expression.
Path analysis and SEM and co-admissing structure analysis hypothesis model expressions such as
X1 = a1 * X2 + e1
X3 = a2 * X1 + a3 * X4 + e2
to calculate values of a1, a2, and a3, and to verify the goodness of the data to this model expression.
LiNGAM's breakthrough is that it can guide model expressions from data without the need for an analyzer to place them. Amazing.
LiNGAM is a prerequisite for the nonnormal distribution of the error e and the relationship between the variables being linear sums.
Therefore, if the data is uniformly distributed and this condition applies, the values of coefficients such as a1, a2, and a3 are quite neatly determined.
LiNGAM is a way to automatically guide a path analysis model without a person having to decide.
When used as an analysis of variable mates, you can be peered by whether the sides are connected or not.
In LiNGAM's general commentary, it seems very often that "the direction of causality can be understood only from data".
But the rationale is that the prerequisites are in place.
I think that it is misuse if it is insisted that "The direction of causality is understood only from the data" in any data and any causal relationship.
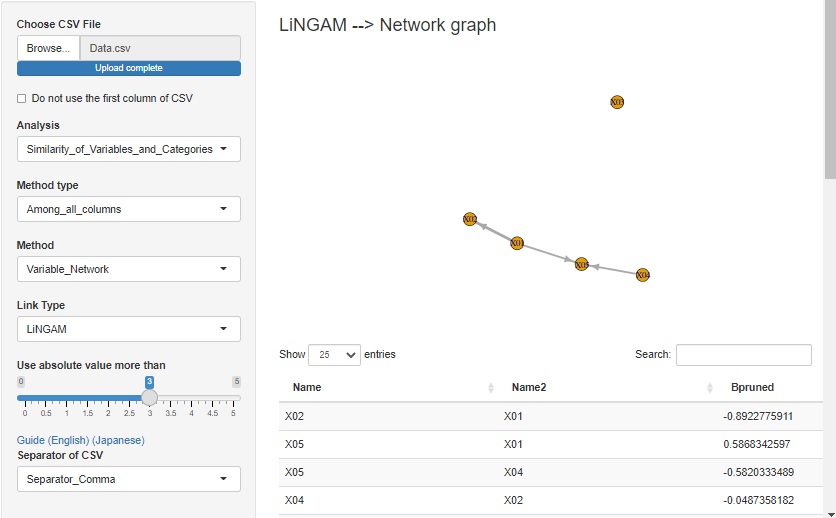
Example of R is in the page, LiNGAM by R .
R-EDA1
has LiNGAM function.
NEXT 
Distribution for which LiNGAM is effective
