トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

回帰分析への測定誤差の影響

一般的なデータには、 測定の誤差 があります。 これによって、「正確に測定することができれば5.2だが、データとして持っているのは5.4」、といったことが起きます。 これは、「真の値は、わからない」と 統計学 でよく言われている話と同じです。

このページでは、測定誤差が回帰分析にどのように影響しているのかを見るために、 ばらつきモデル を使った シミュレーション をします。 こうすると、「真の値だったらどうなる？」という、現実のデータでは確認できないことが確認できます。

真の値による回帰分析

下の ヒストグラム のデータがあったとします。 サンプル（N数）は1000個あります。 これは、平均値が0、標準偏差が1になる 正規分布 になっています。

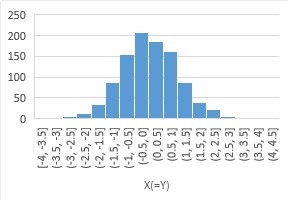
ここで、Yは、Xと同じ数字だったとします。 すると、 ２次元散布図 では、データがきれいな直線上に並びます。 単回帰分析 をすると、
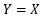・・・(1)
という式が狙い通りに求まります。

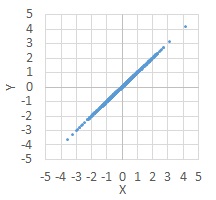
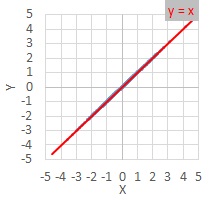
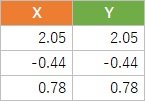
データの表は、1000個のサンプルの内の、3個です。 XとYが同じ数値になっています。

データに測定の誤差があると

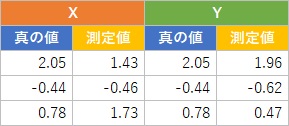
上の話のデータを「真の値」として、これに、平均値が0、標準偏差が1になる測定の誤差を足し合わせて、測定の誤差が含まれているデータを作ります。 XにもYにも、この誤差があるとします。 表のデータは、1000個のサンプルの内の3個の例です。

真の値の時は、XとYのデータは同じ数字になりました。 しかし、測定値の場合、XとYで真の値が同じでも、別々に測定されたものと考えるので、 例えば、「真の値は、XもYも2.05、測定値のXは1.43、Yは1.96」という状況が起きます。

そして、このデータで散布図を作って、回帰分析もするのですが、XとYにそれぞれ真の値と測定値があるので、それらの組み合わせで、 4通りのグラフができます。

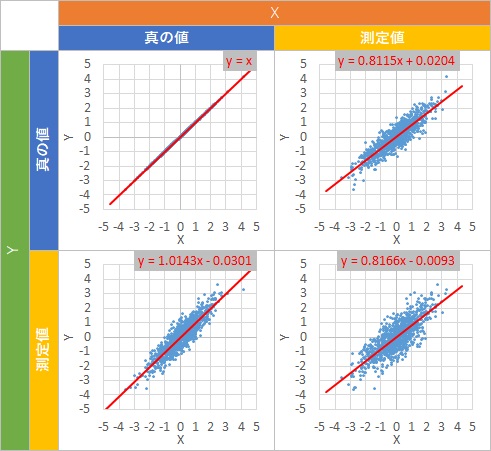
この4通りのグラフに共通するのは、Y切片が0か、ほぼ0になっていることです。 つまり、原点を通るグラフになっています。
傾きは大きく分けると2種類があります。 左上のXもYも真の値の時は、傾きが1ですが、左下のXが真の値でYが測定値の時も、傾きはほぼ1です。 ところが、右上と右下のXを測定値にしたものは、傾きがほぼ0.81で、緩くなっています。

気持ちとしては、XとYが測定値だったとしても、測定値から求まる式と、真の値から求まる式は近いものになって欲しいです。 しかし、Xが測定値の場合は、傾きが緩くなった式が求まることがわかります。

一般的なデータには、 測定の誤差 があるとすれば、回帰分析の方法では、真の値から求まる式よりも傾きが緩い式しか求まらないことになります。

思ったようにならない別の例

上の例は「測定の誤差」という現実のデータに付いてくることを例にしました。

回帰分析で、思ったような数式が求まらない例としては、もっとシンプルな例もあります。

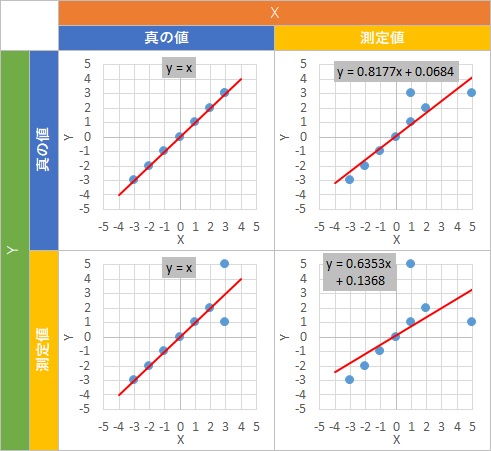
この例でも、気持ちとしては、4つのパターンのすべてで、
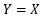・・・(1)
という式が求まってほしいです。 しかし、X方向にばらついている時は、傾きが緩やかになります。 Y方向にばらついているだけなら、欲しい式が狙い通りに求まるところがポイントです。

回帰分析のモデル式

単回帰分析 では、
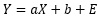・・・(2)
という式が仮定されて、使われています。 「E」の部分を書いている文献は、少ないと思います。 Eがない式の係数aとbの具体的な数字を求めるのが単回帰分析ですが、ばらつきのある実際のデータが当てはまる式としては、Eの部分が必要です。

この式の意味は、「Xに定数aを掛け合わせたものに、定数bと誤差Eが足し合わされたものがYの値になっている」です。 Eの部分に、直線からデータがばらつく分が含まれるようになっています。

一般的な回帰分析では、誤差Eは、正規分布を仮定します。

Xが真の値でYが測定値の時は、真の値だけの式とほぼ同じになる理由

真の値と測定値の組み合わせを見た時に、Xが真の値でYが測定値の時は、真の値だけの式とほぼ同じ式が求まりました。

(1)式を見ると、ちょうどaが1で、bが0の時は、右辺は、Xの真の値に誤差が足されている式になります。 一方で、左辺は、Xの真の値と同じ数値に、誤差を足して作ったものです。

aが1で、bが0の時というのは、測定値と真の値の関係を表すことになります。 これは、データの実際の背景と同じになるため、aが1、bが0という数値が求まって来る、と考えられます。

Xが測定値の時は、真の値だけの式と異なる理由

上記の話ですが、見方を変えると、(1)式というのは、Yだけが測定値になっていて、誤差が含まれている時のモデル式と言えます。

Xが測定値の時は、このモデル式の想定と異なってしまうので、aが1に近くならないと考えられます。

もっと一般的な場合

このページの例は、直線にぴったり乗るデータが真の値になっています。

例えば、2次曲線にぴったり乗るデータが真の値なのに、(2)式を使って、aやbを求めようとすると、 2次曲線と直線の違いによる"誤差"も、Eの部分に入って来ます。

回帰分析のモデル式の理解からわかること

回帰分析では、直線の近似では良くない時に、より複雑な関数を使うことがあります。

また、「誤差Eを正規分布で近似することの妥当性」が注目されることもあります。 正規分布ではない回帰分析として「 一般化線形モデル 」があります。

いずれにしても、回帰分析の枠組みに、Xの測定誤差がある点が含まれていない点は変わらないです。

XとYの測定の誤差の大きさは、回帰分析に使うデータとは別に、調べてみないとわかりません。 また、わかったとしても、モデルに組み込むべきかは、ケースバイケースと思います。 どう組み込むのか？、という課題もあります。

測定の誤差というのは、「同じものを繰り返し測って標準偏差を見る」ということは簡単にできますが、 データサイエンス の中での扱い方は、けっこう難しいものと思っています。

測定の誤差以外の「誤差」の影響

このページでは、議論のわかりやすさから、「測定の誤差」だけで話をまとめました。

しかし、測定の誤差は、非常に精度が高くても、 直線や、曲線にピッタリ乗るデータが得られることは、普通はありません。 ピッタリに近くはなっても、多少、ばらつきます。

測定の誤差以外の「誤差」の影響と考えられますが、この場合も、XとYの両方に「誤差」の影響があることは同じです、

LiNGAM

順路 次は 比例分散の回帰分析