ヒストグラム

ヒストグラムは１次元分布のグラフの仲間です。 1次元散布図と似た分析ができますが、こちらはデータの密集度を、棒の長さにして表現します。

「正規分布かな？」といったことを調べるのに便利です。

なお、ヒストグラムは、 QC７つ道具のひとつという位置付けで、品質管理の分野では啓蒙されています。

強み

ヒストグラムでは密集の度合いが、簡単にわかります。密集している所を見つけたい場合には便利です。

散布図は、データ数が膨大になって来ると、点の密集地帯の様子がわからなくなります。ヒストグラムは、散布図の弱点をカバーする使い方ができます。下の２つのグラフはデータが同じです。
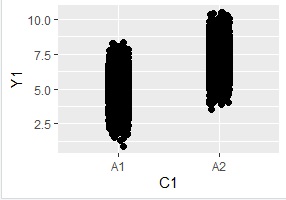
一次元散布図（ジター）

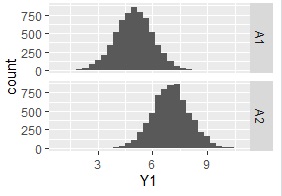
ヒストグラムでは、サンプル数が非常に少ない領域で、サンプルが得られていることが、見えにくくなってしまいます。そのため、外れ値の判定では、うまく使えないことがあります。この弱点が気になる時は、箱ひげ図や一次元散布図の方が良いです。下の２つのグラフはデータが同じです。
ヒストグラム

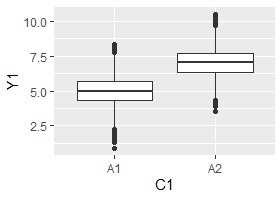
ヒストグラムはそれぞれの棒に範囲があります。これを工夫すると、とても便利なグラフになります。

ヒストグラムは、区間の区切り方にコツがあります。

品質管理の教科書を見ると、最大値と最小値を、適当な数で均等に分割する方法が説明されていることがあります。いろいろなソフトのデフォルトは、この決め方になっています。

図の例は、最大値が267.7558、最小値が38.3496です。
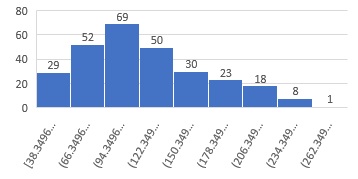
ヒストグラム1

この方法は、とりあえず分布を見るには良いのですが、横軸の数字がとても細かくなりやすいのが欠点です。「234.349と262.349の間に、8個データがある」、と言われても、ピンと来ないです。説得力がなかったり、議論が進めにくいグラフになります。

また、合否判定の値がある場合、不合格品がいくつあるのかが、数えられないです。

もうひとつの図は、筆者がよく使う形です。区間が区切りの良い数字になっています。例えば、210以上が不良品になるのなら、「9,5,4,5,2,2」を足した数が不良品の数になることも簡単に計算できます。
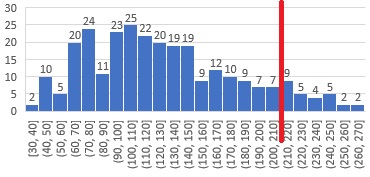
ヒストグラム2

こういうヒストグラムの作り方は、ソフトによって違います。共通しているのは、区切りの良い区間を直接設定できるようになっているソフトはないので、データの加工や複数の設定を組み合わせて、区切りの良い区間を設定する必要がある点です。

上記の例は、Excelで作っていますが、詳しくは Excelのヒストグラムにまとめました。 ggplot2 と seaborn での作り方は、それぞれのページにまとめました。

ggplot2 では、Excelと似ていて、桁数の加工が必要ですが、Excelより簡単です。 seaborn やStatworksは、桁数の修正をしなくても良いので、もっと簡単です。