このサイトでは、データの構造を表す時に、 ネットワークグラフ を、よく使っています。 これは、広い意味でのグラフィカルモデリングです。
データの構造は、言葉や数式で表現することもできますが、グラフィカルモデリングをすると、直感的な理解をしやすくなります。 因果推論 では重宝します。
グラフは絵ですが、これを作るためのデータの書き方には約束事があります。
有向グラフの場合です。
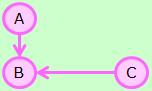
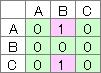
無向グラフの場合は、対称行列です。
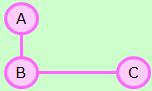
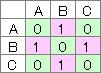
詳しい説明は、 ネットワークグラフ のページにあります。
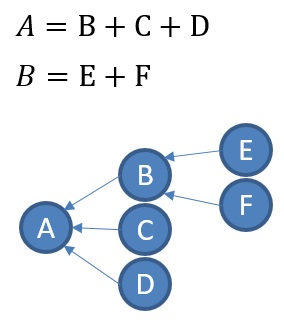
数式をグラフで表した例が、上図になります。
グラフからわかるのは、「Aに直接関係しているのは、BとCとD」ということで、B、C、Dのどういう数式なのかということまでは、 表現できていませんが、グラフにすると、視覚的に理解しやすくなります。
数式をグラフにする場合は、行列を経由しますが、上の例の場合の行列が下になります。
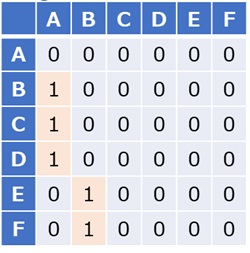
グラフィカルモデリングと、 スパースモデリング は、とても相性が良いです。 グラフィカルモデリングは、 スパースモデリング の結果を、わかりやすく表現する方法になります。
グラフィカルラッソ のように、グラフィカルモデリングと数学的に高度な数学的の理論を組み合わせたようなものもありますが、 「係数の小さなものは、誤差とみなしてゼロにしてしまう」というスパースモデリングもあります。
「ゼロにする」というところは、人によっては、とても抵抗感が出てしまうところです。
実際のところ、「いくつ以下をゼロにするか」というところで、結果の見え方がガラッと変わることがあるので、その抵抗感はもっともなところでもあります。
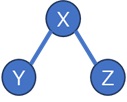
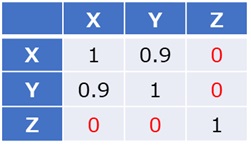
例えば、相関係数を計算すると、以下のようになったとします。
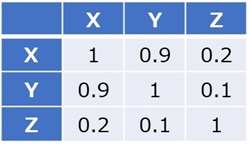
これについて、「0.1以下は無視する」という方針にすると、下のようになります。
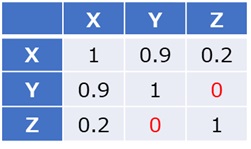
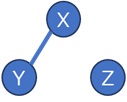
「0.2以下は無視する」という方針にすると、下のようになります。
「グラフィカルモデリング」で文献を探すと、関係を表すものが、偏相関係数の場合だけだったり、 それよりも少し広げて、条件付き独立の話をしていることが一般的のようです。 このサイトでは、このケースを「狭義」と呼ぶことにしています。
「広義」としては、関係を表すものは何でも良いと考えます。 このように考えると、グラフィカルモデリングは、 広い意味での ネットワーク や、 圏論（カテゴリーの理論） の話に守備範囲が広がります。
以下の３冊は、 偏相関 のグラフィカルモデリングを解説しています。
「グラフィカルモデリング」 宮川雅巳 著 朝倉書店 1997
タイトルに「グラフィカルモデリング」とある専門書です。
数理の理解を深める内容になっています。
「Excelで学ぶ共分散構造分析とグラフィカルモデリング Excel2013/2010/2007対応版」 小島隆矢・山本将史 著 オーム社 2013
共分散構造分析とグラフィカルモデリングを一冊の中で解説しています。
実際に動かすことまで重視した内容になっています。
「多変量解析法入門」 永田靖・棟近雅彦 共著 サイエンス社
グラフィカルモデリングについて、
数ページでコンパクトにまとまっています。
順路
次は
３次元のグラフ
