サンプルの類似度の分析

サンプルの類似度の分析では、データの表を横に短冊状に切って、短冊同士の近さを見ます。
関係性の行列表現

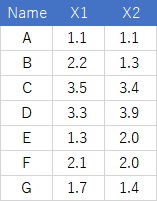
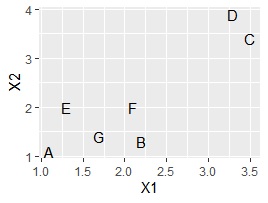
下のようなデータがあったとします。言葉の散布図を作ると、C、Dの2つと、他の5つのグループに分かれるように見えます。サンプルの類似度の分析では、こういったデータの見方をします。
k-means k-means

多次元の場合

上の例は、データが２次元（変数が2つ）の場合のやり方です。２次元だと、２次元散布図でサンプルの類似度の分析ができます。

３次元以上の場合もに、２次元のすべての組合せを、２次元散布図で見てみることはできます。しかし、この方法だとグラフがたくさんできるので、「結論はこうです」ということを直接表すグラフにはならないので、人に説明する時に伝わりにくいです。

多変量解析やデータマイニングの中には３次元以上でも仲間分けができるようにする方法があります。

「高次元を２次元に圧縮して可視化する方法」と、「クラスター分析（グループ分けの結果を教えてくれる方法）」の２種類があります。

高次元を２次元に圧縮して可視化する方法では、高次元問題を２次元問題にしていきます。 100次元あって、どうしようもない感じになっている問題でも、２次元分だけを見れば良いことになるのなら、分析できるようになります。

散布図を使う方法は、人が「これとこれは近い」といった検討をする時に使えます。グループ分けをしたい時は、人がラベルを付ける必要があります。

クラスター分析は、グループ分けの結果を自動で出してくれます。サンプルの数が多い時に便利です。

また、クラスター分析の内、階層型の手法の場合は、デンドログラムという、散布図とはまったく違うグラフで、サンプルの近さを表現します。このグラフは、近さの情報だけを表すこともあり、多次元の情報でも、2次元上（平面上）に表すことができます。

サンプルの類似度の分析の方法は、特徴量エンジニアリングとしても応用ができます。高次元を２次元に圧縮して可視化する方法と、クラスター分析は、「ツートップ」や「双頭の竜」とも言えるような関係になっています。量的変数に圧縮する場合のベストと、質的変数に圧縮する場合のベストです。

高次元を２次元に圧縮して可視化する方法は、１次元や３次元に圧縮することもできますが、１次元だと情報の欠落が多過ぎて必要な分析ができなくなることが多く、３次元だと視覚的な分析が難しいです。そのため、視覚的な分析を目的とした、量的変数への圧縮は、２次元が一番使い勝手が良いです。

特徴量エンジニアリングを目的としたクラスター分析の応用は、ベクトル量子化と呼ばれています。質的変数にすると、数値的な連続性が扱えなくなりますが、複雑な分布をざっくりと捉えることが割と簡単にできるようになります。１次元の質的変数は、２次元の量的変数では表現できない情報が扱えます。

サンプルの類似度の分析では、サンプルの類似度を、距離で評価します。距離のページに詳しく書きましたが、距離の考え方は、これだけでも奥が深いです。