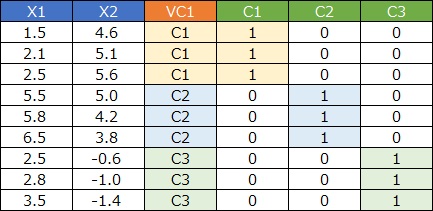
ベクトル量子化は、 クラスター分析 を応用した 量的データを質的データに変換 の方法です。
例えば、下のようなデータがあったとします。
散布図を見ると、３つの領域に３つずつサンプルがあるように見えます。
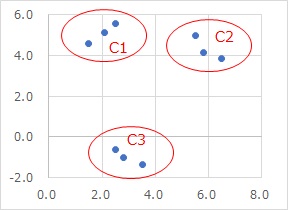
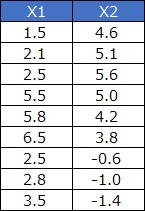
「１行目のサンプルは、散布図のここ」と言った感じで手作業でデータを分類するのは大変ですが、 クラスター分析 を使うと、その作業が簡単にできます。
ベクトル量子化は、その作業の結果を新しい変数として作ったものです。
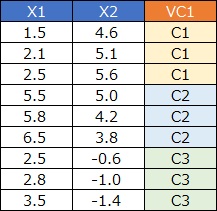
高次元を２次元に圧縮して可視化 のように、多変量問題（高次元）を少変量問題（低次元）に変換して、効率良く、効果的に分析するアプローチは、よく知られています。
２次元に圧縮する技術は、１次元に圧縮もできるのですが、１次元だと、失われる情報が多過ぎて、役に立たないことが多いです。
ただし、「１次元に圧縮すると良くない」というのは、量的変数に圧縮する場合です。 ベクトル量子化は、高次元を１次元に圧縮する方法ですが、質的変数に圧縮します。 質的変数にすると、カテゴリ間の順番の情報が入らなくなります。 そのため、データの連続性は扱えなくなるのですが、その代わり、「データを粗く見る」という点では、優れた方法になっています。
１次元クラスタリング
を上記と同じデータに使うと、例えば、下図のようになります。
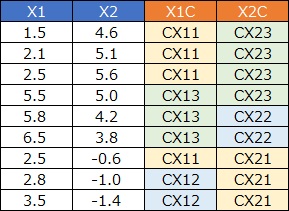
１列ずつを、質的変数に変換しています。 これはこれで使い道があり、 カテゴリの類似度の分析 などに持ち込めるのですが、「３つの領域に分かれている」ということは、表現できない方法になっています。
ベクトル量子化は、もともと通信関係の分野で、データを圧縮する方法として使われて来たようです。 文献を探すと、通信関係でかなり古いものがたくさんありました。
高次元で、無限のパターンがある細かな数字が、クラスターの数だけしかない１次元データに変わるので、相当な圧縮ができます。
データ分析をする時の 特徴量エンジニアリング としての使い道もあります。
まず、質的変数のままでも使い道があり、 ベクトル量子化平均法 です。
ダミー変換
をして、量的変数に変換すると、使い道が増えます。
目的変数が質的変数でロジスティック回帰分析をする時に、説明変数の前処理にこの方法を使っているものは、
下記の参考文献に載っていました。
このサイトでは
ベクトル量子化ロジスティック回帰分析
のページで紹介しています。
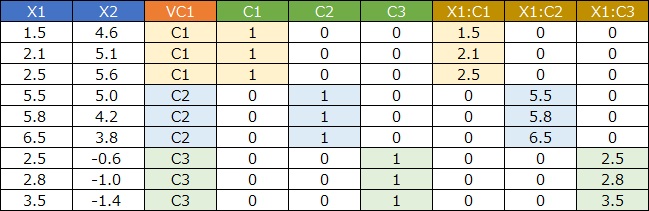
ダミー変数と元のデータの
交互作用項
を作ると、さらに使い道が増えます。
ベクトル量子化回帰分析
は、説明変数の前処理として、この方法を使っています。
目的変数が量的変数の場合は、交互作用項を作った方が精度が上がります。
「１次元を高次元にする方法」と聞くと、筆者の感覚では「そんなことができるのか？」、「できたとして何の役に立つのか？」と思いたくなるのですが、 そう思ってしまうのは、量的変数の変換のイメージが強いからのようです。 理解の仕方としては、「１次元の質的変数のままだと、数値的な処理が使えないので、多次元に変換してから使う。 多次元になっても、入っている情報は１次元の質的変数と同じ」とすれば良いようです。
Rによるベクトル量子化平均法 、 Rによるベクトル量子化ロジスティック回帰分析 、 Rによるベクトル量子化回帰分析 のページがあります。
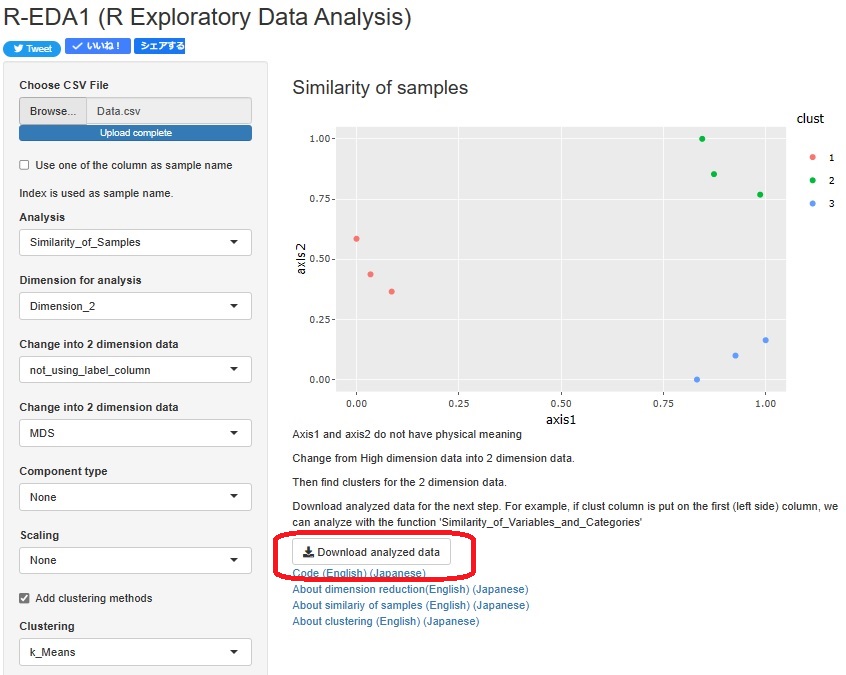
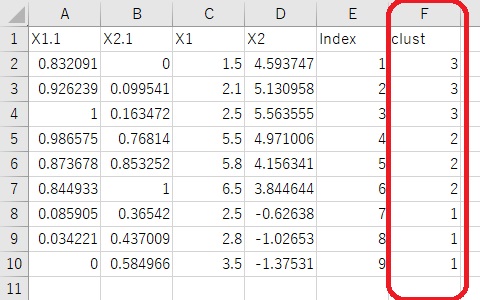
R-EDA1
では、クラスター分析の後で、「Download analyzed data」というボタンを推すと、クラスターの番号を変数にしたデータを出力できます。
クラスターの作り方は、データに対していきなりクラスター分析をする方法と、
下図のように、高次元データを２次元データに圧縮してから、クラスターを作る方法の２通りができます。
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
７章は、
ラベル分類
に、k-means法を応用する方法を紹介しています。
まず、ベクトル量子化で、複雑なデータをk-means法で処理する方法を紹介しています。
その後で、k-means法で処理したデータを説明変数として、
ロジスティック回帰分析
をすることで、ラベル分類をしてます。
k-means＋ロジスティック回帰分析は、学習が早くて、結果の保存が楽。
あるモデルの出力を別のモデルの入力にする方法は、「モデルスタッキング（model stacking）」と呼ばれる。
線形分類器と、非線形分類器の両方の利点を利用できる。
k-meansを使う時は、データのグループ分けが目的なのが一般的であり、その場合は、kをいくつにするのかがポイントになる。
ロジスティック回帰分析の前処理としてk-meansを使う場合は、連続的に広がっている分布を分割して把握するためなので、
kの数はあまり問題にならない。
「Pythonではじめる機械学習 scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」 Andreas C.Muller, Sarah Guido 著 オライリー・ジャパン 2017
ベクトル量子化の紹介をしてから、k-means法を分類問題に使う話をしています。
抽出する成分の数を、次元の数よりも多くできるのが、k-means法を使った場合の特徴。
10個のクラスターができた場合、０と１を使った変数を作ることで、10個の新しい変数ができることになる。
これを使うと、複雑な分布を線形モデルで分離できる。
この本は、
主成分分析
や
NMF
と同じように、k-means法がデータ圧縮や成分分解としての使い方があることを紹介してから、k-means法の利点が出る方法として、
複雑なデータの分類問題を紹介しています。
この分類問題の話だけなら、
「機械学習のための特徴量エンジニアリング」の本の方が、詳しく書かれています。
「音声認識」 篠田浩一 著 講談社 2017
音声特徴量は、数10次元になる。
k-means
などでグループ分けして、グループ名を記憶するようにすると、1次元の特徴量となって、記憶領域の節約になる。
これをベクトル量子化と呼ばれる。
「情報理論の基礎 情報と学習の直観的理解のために」 村田昇 著 サイエンス社 2008
ベクトル量子化の方法として、k-means法とLVQ（Learning Vector Quantizationf4r）を紹介しています。
順路
次は
微分データと積分データ
