上のようなデータがあったとします。 Yが1と0の２つあり、X01、X02という変数があります。 Yが1は、２つの領域に分かれていて、Yが0は、その間にあります。
複数の変数があるデータについて、 クラスター分析 をして、個々のサンプルのクラスターを求め、そのクラスターの名前をカテゴリにした質的変数にして使う方法を、 ベクトル量子化 と言います。
ベクトル量子化平均法というのは、適当な名前が世の中にないようなので、筆者が付けました。 ベクトル量子化をした説明変数と、目的変数の関係を分析する方法です。
判別分析 や ロジスティック回帰分析 と類似の分析です。
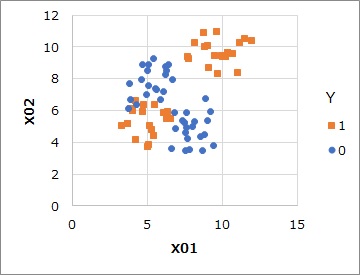
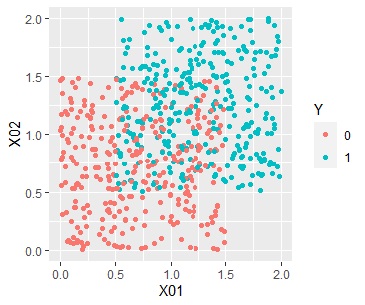
上のようなデータがあったとします。
Yが1と0の２つあり、X01、X02という変数があります。
Yが1は、２つの領域に分かれていて、Yが0は、その間にあります。
Yを抜いたX01とX02の２つの説明変数だけで、クラスタリングをします。
この例では、混合分布法で３つの領域に分かれました。
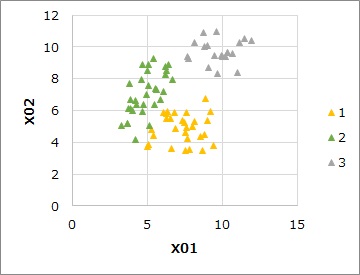
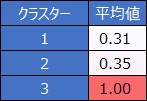
クラスター毎にYの値の平均値を計算します。
１と０しかない変数なので、平均値は、１の割合（確率）として計算されます。
このモデルはいまいちで、クラスター３のサンプルはきれいに分離できているのですが、クラスター１と２はあいまいな分離になっています。
この例の場合は、説明変数が２個なので、例えば散布図の位置がクラスター２のあたりにあるサンプルは、Yを１と予測する確率が0.31なので、予測値は０です。
ちなみに、このページは、「新しいサンプルは、２値のどちらなのか？」ということを調べるための方法です。 「新しいサンプルは、どのクラスターになるのか？」ということを調べる方法は、 クラスターの予測の分析 になります。 順序としては、「新しいサンプルは、どのクラスターになるのか？」をしてから、上記の平均値を使って、「新しいサンプルは、２値のどちらなのか？」を調べます。
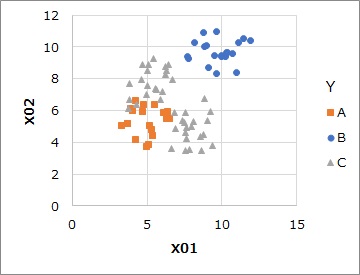
例えば、上のような３値の場合は、分析は下の表になります。
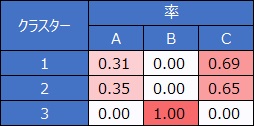
２値の場合は、平均値を計算します。 目的変数が量的変数の場合に、この方法はそのまま使えます。
下記は、左が元データで、右が予測値です。
クラスターが同じだと、予測値が同じなので、結果的に粗い予測値になっています。
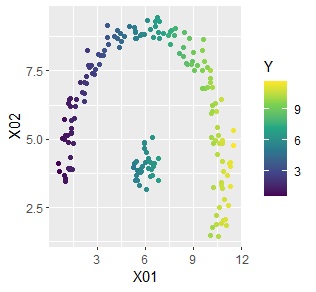
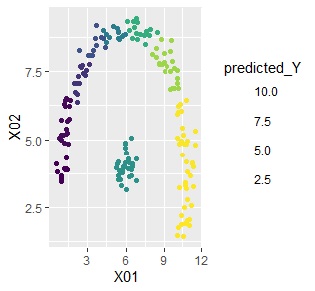
ベクトル量子化平均法の使い道として、一番有望なのは予測です。 複雑な分布でも対応できます。
ベクトル量子化平均法は、複雑な分布でも予測精度が高い方法ですが、 説明可能性・解釈可能性 がないので、因果推論 には使えないです。こうした特徴は、 k近傍法 と似ています。 ちなみに、ベクトル量子化平均法は、全部のサンプル間の距離を調べないので、計算はk近傍法よりも早いです。
別の使い道としては、データの偏りの分析があります。
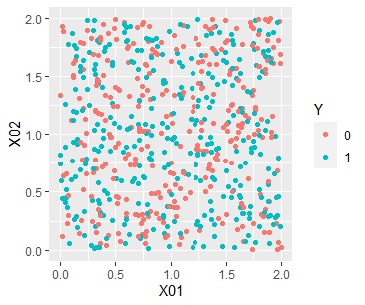
例えば、２種類の分布があって、左のように２値が均等に混ざっている感じの場合（Data1）と、右のように領域がだいたい分かれている場合（Data2）があったとします。
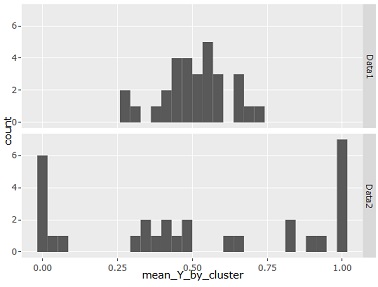
この場合、クラスター毎の平均値をヒストグラムにすると、下図のようになります。
偏りがないと、0.5付近が多く、偏りがあると、0や1に近い値が増える様子がわかります。
こうした偏りは３次元までなら、グラフを見ればわかりますが、高次元の場合は、ベクトル量子化平均法が良いようです。
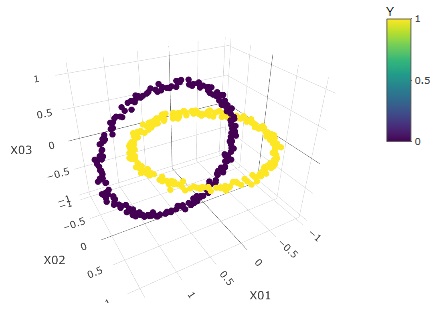
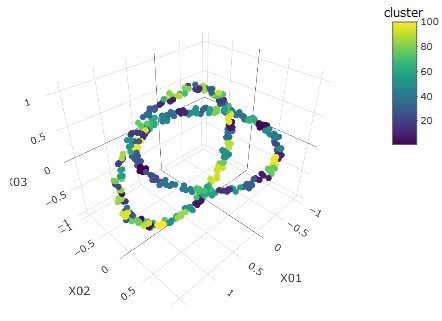
下のグラフは、左から順に、元データ、クラスター、予測値です。
クラスターは100個作っています。
こういう複雑な分布でも、ベクトル量子化平均法は、完璧に予測できることがわかります。
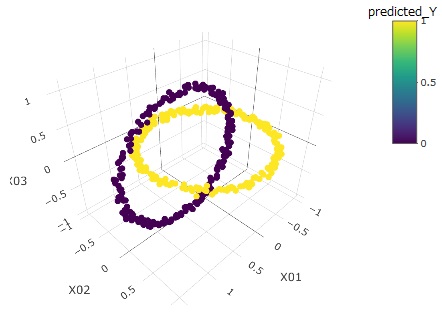
上記の方法は、目的変数が２値データでも、量的データでも使えます。
上記以外で ベクトル量子化 を活用する方法として、下記があります。
ベクトル量子化ロジスティック回帰分析 は、目的変数が２値データの時の方法です。
このクラスターを使った計算の結果が下のグラフです。
下のグラフは左から順に、ベクトル量子化平均法、ベクトル量子化ロジスティック回帰分析です。
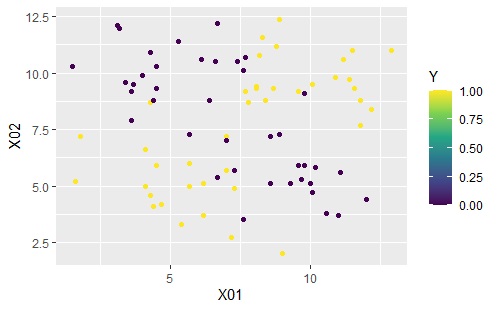
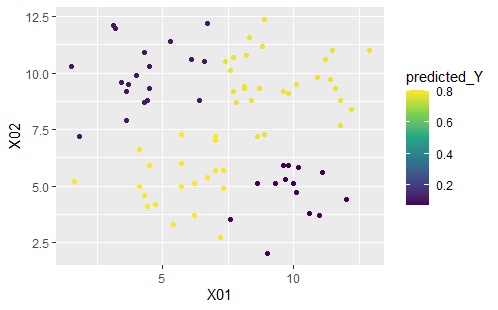
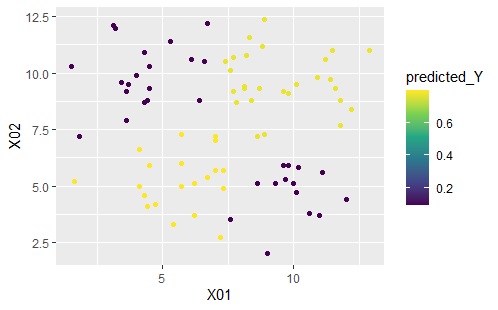
結果に違いはないです。
それぞれのクラスターの中で、説明変数に応じた傾きがある場合は、ベクトル量子化平均法よりも、 ベクトル量子化回帰分析の方が精度が良いです。
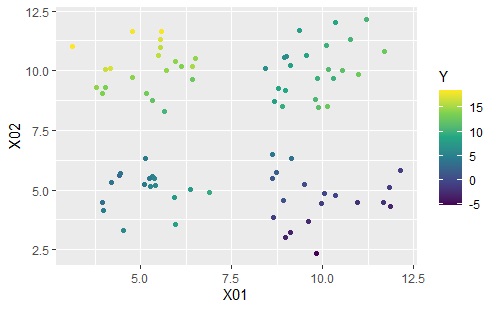
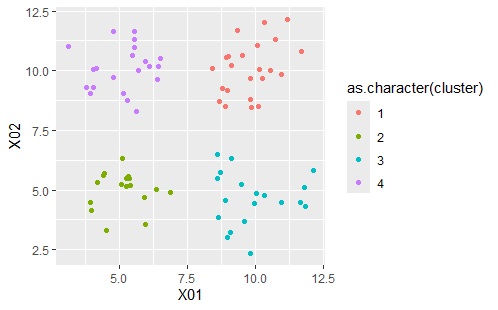
上のグラフは左から順に、元のデータ、クラスター分析で４つのクラスターを作った場合の結果です。
このクラスターを使った計算の結果が下のグラフです。
下のグラフは左から順に、ベクトル量子化平均法、ベクトル量子化回帰分析です。
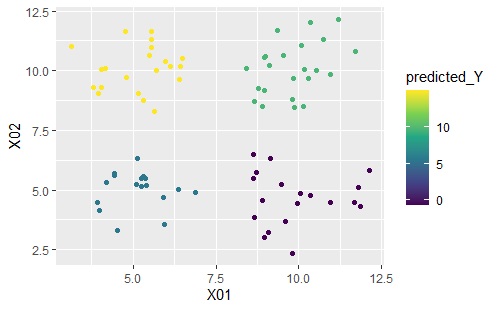
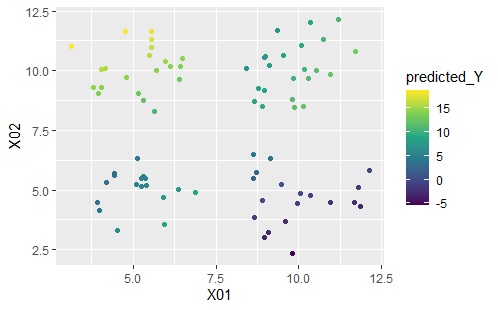
ベクトル量子化平均法は、同じクラスターの中では同じ値になっていることがわかります。
一方、ベクトル量子化回帰分析は、元のデータを精度良く予測できています。
Rの実施例は、 Rによるベクトル量子化平均法 のページがあります。
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
この本では、k-means法とロジスティック回帰分析を組み合わせることで、複雑な分布になっているラベル分類をシンプルに解く方法として紹介しています。
このページの「ベクトル量子化平均法」という方法は、この本を読んだ後で、「ロジスティック回帰分析を使わずに、もっとシンプルにできる」ということに
筆者が気付いてまとめたものです。
探せば、世の中に同じ方法があるかもしれないです。
順路
次は
外れたサンプルの探索
