という形をしています。
左辺は、 ロジット です。 左辺を Z と置いてしまえば、普通の 重回帰分析 と同じ形になります。 図の例では、Xがひとつなので、
の式を使っています。
pを縦軸に、Xを横軸にしてグラフにすると、このページのようなカーブになります。
ロジスティック回帰分析は、Yが「ON」と「OFF」のように、質的データになっている時の分析方法です。 「 回帰分析 」となっていますが、中身や使い道がかなり違います。
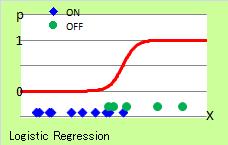
図は、ロジスティック回帰分析の図です。 カーブが表しているのは、 「Yが、Xによって、ONやOFFになる確率」です。 p は、OFFが発生する確率です。 1-p は、ONが発生する確率を表します。
プロットは、ONとOFFの１次元散布図です。 同じグラフに重ねてみました。
この図では、Xが大きいと1に近くなるということから、Xが大きいとYがOFFになる確率が高いことがわかります。
例えば、「OFF」の確率が0.9なら、「ON」の確率は0.1という意味です。 これは、同じXの値に対して、「OFF」が9回起きて、「ON」が1回起きるという意味です。
ロジスティック回帰分析の式は、
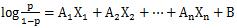
という形をしています。
左辺は、
ロジット
です。
左辺を Z と置いてしまえば、普通の
重回帰分析
と同じ形になります。
図の例では、Xがひとつなので、
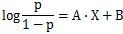
の式を使っています。
pを縦軸に、Xを横軸にしてグラフにすると、このページのようなカーブになります。
もともとのYはONとOFFですが、この値とXの値を使って、pとXの関係式を求めます。
ロジスティック回帰分析は、結果は良いとしても、「なぜ、こんな計算をする？」と思ってしまいます。
統計的にもっとわかりやすく、ロジスティック回帰分析とよく似たものに、 プロビット を使うプロビット分析があります。
Yが、「ON」と「OFF」を例にしましたが、 ロジスティック回帰分析は、この例のように、相反するカテゴリがYになっている場合に適しています。 例えば、「あり・なし」、「起きる・起きない」、「良品・不良品」等です。
例えば、「トマト」と「キャベツ」がYになっている場合は、そのデータの中には、２つのYしかなくても、 「キュウリ」や「ジャガイモ」等、他にも考えられますので、このようなカテゴリの場合は不向きです。
ロジスティック回帰分析がよくできているのは、 確率のデータの特徴を、数式で表現できていることです。 多変量解析 にはいろいろありますが、確率を扱うのに適した手法は、筆者の知る限り、他にはありません。
意思決定論 、 リスク評価 、 人工知能 といった分野では、確率を使うことが重要です。 昨今、ロジスティック回帰分析の解説をよく見かけるようになりましたが、その理由はこの辺りになるようです。
ロジスティック回帰分析は、統計学や機械学習の様々なソフトに入っています。 プロビット分析は、Rではできますが、それ以外のソフトで筆者は見かけた記憶がありません。
上記の方法は、 Rによるロジスティック回帰分析のページがあります。
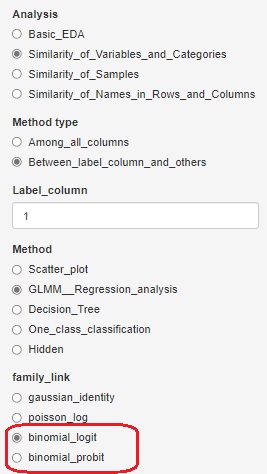
R-EDA1 には、「ロジスティック回帰分析」や「プロビット分析」という項目はないのですが、 一般化線形混合モデル（GLMM） の機能のひとつとして、 ロジスティック回帰分析と、プロビット分析ができるようにしてあります。 「family_link」で、「binomial_logit」を選ぶとロジスティック回帰分析、「binomial_probit」を選ぶとプロビット分析ができます。
GLMMは、散布図を描くツールと、１変数と他のすべての変数の関係を調べるツールのそれぞれに入っています。
「人文・社会科学のためのカテゴリカル・データ解析入門」 太郎丸博 著 ナカニシヤ出版 2005
質的データの統計解析や回帰分析の本です。
基本から実践のノウハウまでの知識をカバーしています。
「統計的モデリング／情報理論と学習理論―データと上手につきあう法」 小西貞則・竹内純一 著 講談社 2008
ロジスティックモデルを使った
リスク評価
があります。
順路
次は
ロジスティック回帰分析の仕組み
