確率（割合も）は、0から1までの数字で表されます。 例えば、成功率や不良率（歩留）はこのような数字です。
確率の値を 多変量解析 で扱う時は、そのまま使うより、ロジット変換する方が良い事が知られています。
確率の値をpとします。
このpの
オッズ
の対数
log( p / (1 - p))
は、ロジットと言い、この変換をロジット変換と言います。
対数は、自然対数です。
Excelの関数を使うなら、
=Ln(p/(1-p))
になります。
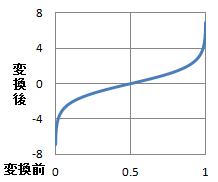
0から1の値を、「p=0.001、0.002、・・・」のように細かく作り、それらを変換した値を作り、
変換前と変換後の値を、散布図にすると、なだらかなカーブになります。
また、変換後の値をヒストグラムにすると、正規分布とよく似た形をしています。
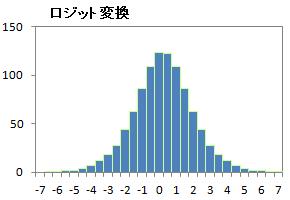
pがぴったり0の場合と、1の場合を計算できないのが弱点です。 その場合は、限りなく0に近い値や、1に近い値を代わりに使う事もあります。
持っているデータを直接ロジット変換しないのですが、ロジット変換を使う有名な 多変量解析 が、 ロジスティック回帰分析 です。 「ロジット分析」とも呼ばれています。
プロビットとは、 標準正規分布 の累積関数の逆関数です。 プロビットを計算する事を、プロビット変換と言います。
Excelの関数を使うなら、
=norminv(p,0,1)
になります。
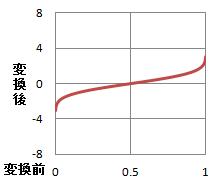
0から1の値を、変換すると、なだらかなカーブになります。
また、変換後の値をヒストグラムにすると、定義通りに標準正規分布になっている様子がわかります。
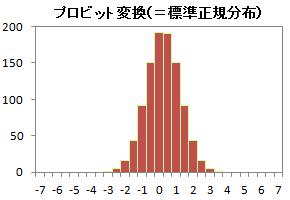
ロジスティック回帰分析 と同様のものとして、プロビットを使う、「プロビット分析」があります。
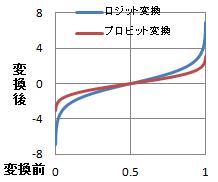
ロジット変換とプロビット変換を比べると、かなり似ています。
グラフを重ねてみると、さらに良くわかります。
ロジット変換の方が、裾野が広いです。
ロジット変換は、自然対数を使って計算します。
対数の底はネイピア数なので、2.7くらいです。
対数の底を5にして、ロジット変換と同じような計算をした場合、つまりExcelで
=log(p/(1-p),5)
で計算した値は、底をネイピア数にした時よりも、さらに標準正規分布に近くなります。
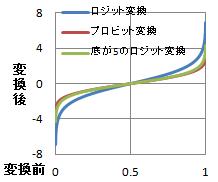
プロビット変換、つまり、標準正規分布の累積関数の逆関数を近似的に計算する方法として、底が5のロジット変換は使えます。
なお、底が5の時は、分布の中心付近は、よく合うのですが、端の方は合いにくいです。 中心付近よりも、端の方の精度が重要な場合は、底は7から9くらいの方が良いです。
プロビットの意味は、計算式が標準正規分布そのものなので、
「確率」という集計値のような値から、集計前のような値を計算していると言えます。
そのため、確率そのものをYにするよりも、起こっている現象を数理的に扱いやすくなる事があるようです。
ロジットは、オッズ比の対数です。 ロジットの意味については、ここから考えるのが順当なはずです。 ただ、 ロジスティック回帰分析 などのデータ解析がロジットを使うと、結構うまくいく説明として、 オッズ比をスタートにして考えても、筆者にはよくわかりません。
それよりも、ロジットが便利な現実的な理由は、 ロジットとプロビットが似ていることではないかと思っています。
0から1までのデータが均等に、かつ、大量にあれば、プロビット変換したデータは、 平均が0で、標準偏差が1になります。
しかし、例えば、pとして、(0.96、0.82、0.69）というデータがあったとします。 これらのデータを、ロジット変換やプロビット変換しても、 平均が0で、標準偏差が1にはなりません。
一方で、この例の値を 標準化 すると、平均が0で、標準偏差が1になります。 つまり、ロジット変換やプロビット変換は、標準化とは異なります。 ただし、別の観点で標準正規分布に近くする変換になっています。
ロジット変換やプロビット変換は、値が0から1までの範囲しかあり得ないデータを、-∞から∞までのデータに変換する方法です。
ところで、例えば、値が0から2までの範囲になっているデータなら、2で割れば、0から1までの範囲になります。 「範囲で割る」という手間を加えると、ロジット変換やプロビット変換は、範囲が有限に決まっているデータを、 範囲が無限のデータに変換する方法として使えます。
また、これとは逆に、逆変換は、無限の範囲から有限の範囲への変換の理論になります。
範囲が無限の理論としては、正規分布を仮定する理論がいろいろあります。 また、範囲が有限の理論としては、フーリエ級数や、確率を扱う理論があります。
これらの変換をする事で、元のデータではうまく使えない理論が使えるようになる可能性が広がります。
順路
次は
オッズとオッズ比
