薬の有無と、病気の有無の関係を表す２×２の
分割表
があったとします。
リスク評価などでは、分割表のデータを使って、各カテゴリの比率（発生確率）の議論に進みます。
こうすると、「比率のpとqの違いは、どうやって評価すれば良いか？」という話ができます。
なお、pやqを使った議論の中では、サンプル数（N数）が考慮されにくいことに注意が必要です。
ちなみに、工業的な分野の リスク評価 では、 発生確率に、発生した場合の影響の大きさを値をかけ合わせた数字を「リスク」と呼ぶことが多いですが、 疫学 などの医学系の分野では、発生確率そのものを「リスク」と呼ぶことが多いです。
pとqの差は、比率の違いの、一番シンプルな指標です。
百分率にして（100倍して）、「今回の選挙では、投票率が5ポイント上がりました」、といった感じで、ニュースなどでも使われる指標です。
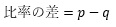
比率の差には、 比率の差の検定 がありますので、データの数も考慮して、「差があると言えるのか？」という分析をすることができます。
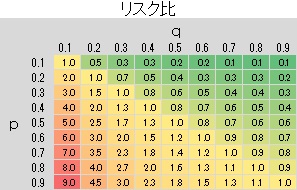
pとqの比は、リスク比や相対リスクなどと呼ばれている指標になります。
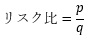
0から無限大までの範囲の値になります。 pとqが同じくらいの値だと、1に近くなります。
オッズは、発生する確率と発生しない確率の比です。
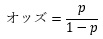
確率は0から1までの値ですが、オッズは0から無限大の値になります。
起きにくいことは0に近く、起きやすいことは大きな値として評価する特徴があります。
不思議な計算をしますが、競馬などのように、「賭けて当たった場合に、どのくらい儲かるのか？」ということをする時には、 良い指標になるようです。
オッズの対数は、 ロジット と呼ばれていて、また別の指標として使われます。 ロジスティック回帰分析 でも使われます。
品質工学 では、オッズと同じ計算式を、「オメガ変換」と呼んでいます。
品質の分野では、確率が０（０％）や１（100％）という数字が普通に存在するのですが、 ０や１はオッズにすると、無限大や無限小になるので使えません。
統計学の理論では、限りなく０に近い確率や１に近い確率はあるのですが、０や１ちょうどの確率がないので、オッズで問題が起きないのかもしれませんが、 品質の分野ではオッズの使い道には工夫が必要な事があります。
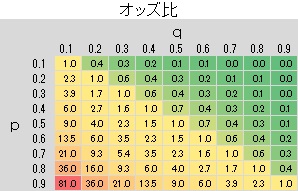
オッズ比は、オッズとオッズの比です。
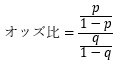
確率は0から1までの値ですが、オッズ比は0から無限大の値になります。
起きにくいことは0に近く、起きやすいことは大きな値として評価する特徴があります。
医学関係では、比率の差の評価は、オッズ比を使うことが慣例化しているようです。
オッズ比の対数をとると、この指標は文字通りオッズ比の対数としての意味もありますが、pとqの ロジット の差としての意味も持ちます。
対数オッズ比の使い道は、後者の意味で考えた方が広がります。
リスク比、オッズ、オッズ比は、 分割表 がなくても、何か別の方法で比率の値を手に入れれば、計算することができます。
ところで、オッズは、上記のpの計算をしなくても、
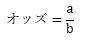
という計算から求めることができます。
また、オッズ比も、上記のpやqの計算をしなくても、
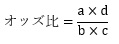
という計算から求めることができます。
何らかの形で、分割表を作ることができれば、比率の値を手に入れることが難しくても、 オッズやオッズ比は計算することができます。
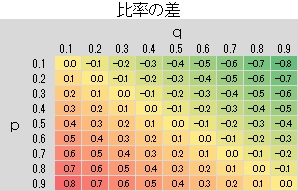
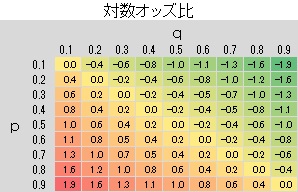
pとqがそれぞれ0.1から0.9までの値を0.1刻みずつ変えた場合に、 各指標の値がどのようになるのかを計算し、 ヒートマップ にしてみました。
比率の差と、対数オッズ比は、右上から左下にかけて、均等に値が増えています。 一方、リスク比やオッズ比は、右上から左下にかけて値が増えることは同じですが、 左下になるほど、急激に値が大きくなっています。 この傾向は、リスク比よりもオッズ比の方が顕著です。
「基礎統計学 栄養科学シリーズNEXT」 鈴木良雄・廣津信義 著 講談社 2012
前向き研究は、何かをしてから結果を見ていく研究方法。
非常に発生確率の低い現象は、調査期間が長く必要になるので大変になる。
後ろ向き研究は、過去に起きたことを見ていく研究方法。
過去の記録がなければできない方法。
後ろ向き研究で、全数の発生状況を調べるのが、後ろ向きコホート研究。
発生した症例をまず集め、それらの症例に背景の近い対照を２人ずつマッチさせて、仮説との関係を見るのが、症例対象研究。
前向き研究や後ろ向き研究は、時間軸の変化を見るので、縦断研究とも呼ばれる。
ある時点での違いを見るのが、横断研究。
オッズは、リスクの有無の指標として便利。
また、オッズは、a/bや、c/dで求められるので、pやqを求める必要がなく便利。
オッズ比は、(a×d) / (b×c)で求められる。
発生確率の低い現象のpやqを求めるには、たくさんの母数が必要になるので、
発生確率が低い現象では、pやqを正確に求めるための調査は不可能なことがある。
そのため、リスク比の計算ができないことがある。
オッズ比は、a、b、c、dの数字があれば求まるので、発生確率が低い現象の指標にも使える。
また、発生確率が低い現象では、オッズ比の値は、リスク比の値と近くなるため、
リスク比と同じような評価ができる。
クロス集計の解析として、比率、比率の差、リスク比、オッズ比の信頼区間や検定。
「すぐわかる統計処理の選び方」 石村貞夫・石村光資郎 著 東京図書 2010
帰無仮説をオッズ比＝１とするオッズ比の検定と、帰無仮説は２つの比率が同じとする
比率の差の検定
が同じ。
また、帰無仮説をオッズ比＝１とするオッズ比の検定と、帰無仮説は２つの事象AとBが独立とする
独立性の検定
が同じ。
「SPSSによるリスク解析のための統計処理」 石村貞夫・石村園子 著 東京図書 2004
オッズ比の計算や、比率の差の検定など。
「基礎からのベイズ統計学 ハミルトニアンモンテカルロ法による実践的入門」 豊田秀樹 編著 朝倉書店 2015
オッズ比は、すべての研究デザインで使用できるが、比率の値の確認も大事。
オッズ比とリスク比の値が近いのは、比率が小さい時だけなので、いつでも同じような解釈に使えるわけではない。
「独習統計学24講 すべての医療系学生・研究者に贈る 応用編」 鶴田陽和 著 朝倉書店 2016
オッズ比の話が、
ロジスティック回帰分析
につながっています。
「カテゴリカルデータ解析 Rで学ぶデータサイエンス」 藤井良宜 著 共立出版 2014
指標は、ピアソンの一致性係数、クラメールのV統計量。
一般化マンテル検定、クラスカルワリス検定、マクマネー検定、オッズ比の均一性の検定など。
「カテゴリカルデータ解析入門」 Alan Agresti 著 サイエンティスト社 2003
相対リスクやオッズ比による解析。
カテゴリカルデータ解析の歴史来な話もあります。
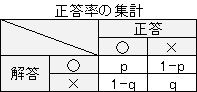
品質工学関係では、率のデータを下の表のように集計して計算します。
リスク評価とは、qの位置が違っています。
混同行列
のページにもありますが、分野によって注目したいものが異なるのが理由のようです。
「エネルギー比型SN比」 鶴田明三 著 日科技連 2016
２種の誤りがある場合のデジタル標準SN比は、
(1/2)*10 (log(p/1-p) +log(q/(1-q))
qの位置をリスク表と同じにすると、この計算式は対数オッズ比と同じです。
「タグチメソッド入門」 田口伸 著 日本規格協会 2016
２種の誤りがある場合のSN比
10 log (pL /(1 - pL))
p0 = 1/((1 + (1/p-1))(1/q-1))^(1/2))
pL = (1 - 2*p0)^2
順路
次は
質的データを量的データに変換
