量的データを質的データに変換 や、質的データを量的データに変換の方法は、 特徴量エンジニアリング のひとつです。 ロバストな解析 でも重要な役割を果たすことがあります。
データサイエンス では、質的データを量的データに変換して、 量的データの手法で扱うことがあります。 単純な変換には ダミー変換 があります。 質的データを ダミー変換 して使う代表的な手法に、 数量化Ⅰ～Ⅳ類 があります。
データの性質や、変換の後に分析したいことによっては、 ダミー変換 以外のアプローチもあります。
質的データの数を数えて、量的データにしたものは、「度数」と呼ばれます。 「頻度」とも呼ばれます。 混同行列 や 分割表 になります。
度数を計算すると、比率が求められます。 統計学 は、比率を「確率」という量的データとして扱います。
0-1データの時系列解析 の方法は、時刻の話を入れ替えれば、時系列データ以外にも応用できます。
「大・中・小」、「当てはまる・どちからと言えば当てはまる・どちからと言えば当てはまらない・当てはまらない」、 「レベル１、２、３、４」など、順序があるカテゴリデータは、順序データと呼ばれます。
「大・中・小」＝「３、２、１」
「当てはまる・どちからと言えば当てはまる・どちからと言えば当てはまらない・当てはまらない」＝「４、３、２、１」
「レベル１、２、３、４」＝「１、２、３、４」
と量的データに変換するのは簡単です。
値の対数的な性質を考慮する必要がある時は、
「大・中・小」＝「100、10、１」
とすることもできます。
こうした変換はとてもお手軽で、とりあえず質的データをグラフにして眺めてみたい時には便利です。
ただし、量的データの間隔に意味がないことに注意が必要です。
質的データが「言葉」の時は、量的データに変換する時に、 数値の境界線をぼかしたいことがあります。 こういう時は、 ファジィ理論 があります。
各カテゴリの頻度を 棒グラフ にした場合、横軸にカテゴリの順序を入れることができます。 ただし、見た目はヒストグラムになりますが、横軸は量的データではないので、ヒストグラムではありません。
リジット変換は、このグラフをヒストグラムとみなしてしまい、確率変数を計算する方法です。 プロビット変換 の逆変換のようなことをします。
質的なデータには、形式が３種類あります。
個々のデータ（観測値）が、「1」と「0」で表現されている形式です。
例は、レシピ毎に、使う材料の「あり」と「なし」を表しています。
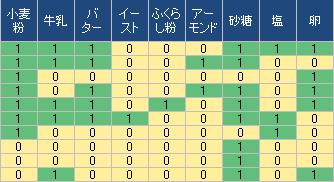
この形式は、質的データを量的データで表しているので、量的データの手法を使うことができます。
個々のデータ（観測値）が、質的なデータになっている形式です。
例は、３つの地点の天気にしてみました。
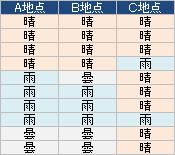
ダミー変換 で、２の形を、１の形に変換することはできます。 しかし、もともと１の形の場合は、値の重複があるため、1の形には変換できません。
各サンプルが、(A,B)、(A,B,C）、(B,D)のようになっている場合です。 この形は、１の形と相互に変換できます。
「すぐわかる統計処理の選び方」 石村貞夫・石村光資郎 著 東京図書 2010
リジット変換や、リジット分析の解説が少しあります。
順路
次は
ダミー変換
