トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

ダミー変換（One-hot encoding）

ダミー変換は、 質的データを量的データに変換する方法です。 量的なデータの解析方法で、質的なデータを解析するのに使います｡

「One-hot encoding」と呼ばれることがあります。

1と0を使った変換

一般的に「ダミー変換」と言えば、1と0を使った変換を呼ぶ事が多いようです。 質的変数を、1と0の量的変数に変えます。

1と0の変換は、説明変数Xの変換に使われることが多いようです。

多変量解析 の方法として、 数量化�T〜�W類 が有名ですが、これらは説明変数Xの質的変数を、1と0の量的変数に変換して計算する方法です。 ダミー変換ではなく、「数量化」と呼んでいます。

1と0を使う利点

ある値に、1をかけると、その値がそのままになり、 0をかけると、その値が0になります。

この性質を使うと、ある変数の「入れる、入れない」を、式で表現できるようになります。

また、コンピュータは基本的に0と1を扱うものなので、 プログラミング の点でも便利です。

変換の手順

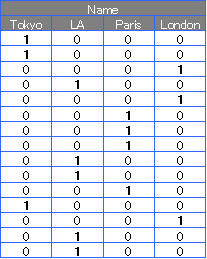ここでは、1列の中に、4種類の名前が入っている例で説明します。

• 4列用意して、4種類の列の項目名にそれぞれの名前を割り振ります。
• 元の列に入っている名前と､新しく用意した列の項目名が一致すれば、「1」、 異なるなら「0」を入れます。

弱点

ダミー変換には弱点があります。

具体例の場合ですと、3つの列が「0」であることと、 残りの列が「1」であることは同値ですので、 多重共線性 の問題があります｡ そのため、使用する時は、どれか1列を解析の対象から外します。

また、名前の数の分だけ列を用意するため、 列の数が増え過ぎる場合があります｡

これらの弱点を避ける方法として、 ２進数変換 もありますが、一長一短です。

ダミー変換の限界を超えるには

質的な説明変数をダミー変数にすると、分析に使える方法が一気に増えます。

これだけでもすごくうれしいのですが、 数量化理論 のページの話があります。 単なるダミー変換では、「Y切片をカテゴリ毎に分ける」ということをするので、思ったほど複雑なモデルにならないです。 量的データになっている他の説明変数とダミー変数の積（交互作用項）を新たな変数にすると、イメージに近いモデルになることがあります。

1と-1を使った変換

1と-1に変換する方法もあります。 1と-1の変換は、 目的変数Yの変換に使われることが多いようです。 これをすると、定量的な理論で パターン認識 ができるようになります。

1と-1を使う利点

例えば、Yが「A」と「B」だったものを、 「1」と「-1」に変換して、量的変数の方法を使ってモデル式を作り、Yを予測するとします。

すると、予測値が0より大きい時は「A」、予測値が0より小さい時は「B」というように、AとBを予測できるようになります。 予測値がちょうど0の時は、AとBの確率が1/2として解釈できます。

予測値が0より大きいか小さいかで、Yを予測するための式は、判別式と呼ばれ、判別のための予測の方法として使われています。

0を判断基準にする方法も、現象を式で表現したり、プログラミングをする時に便利です。

ソフト

Rによる実施例は、 Rによるダミー変換 にまとまっています。

参考文献

「多変量解析の基本と実践がよ〜くわかる本　」 森田浩　秀和システム　2014
判別分析 で、線形判別関数の求め方は、最適化、ラグランジュ未定定数法、 重回帰分析 の3通りを解説しています。
重回帰分析の時のYは、1と-1ではなく、各群のサンプル数を合計のサンプルで割った値に、プラスとマイナスの符号を付けたものを使っています。