２進数変換は、「Binary encoding」という名前が一番メジャーなようです。 「２進数変換」という名前は、呼びやすい日本語名がないようなので、筆者が付けたものです。
質的変数を、0と1を使った量的変数に変換する点は、 ダミー変換 と同じですが、変換の仕方が違っていて、２進数の考え方が使われています。
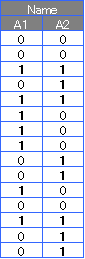
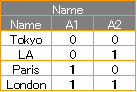
この方法ですと､ダミー変換の２つの弱点を解決することができます。 ダミー変換では、元の１列が４列に増えましたが、 ”２進数”変換では、２列で済みました。
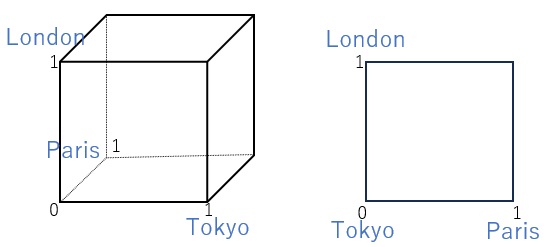
下の絵は、カテゴリが３つの場合の違いを表しています。 左がダミー変換で、右が２進数変換です。
３つを表すのに、ダミー変換は３次元（３変数・１辺１の立方体）が必要で、２進数変換は２次元（２変数・１辺１の正方形）を使っています。
この違いは、次元数の違いは、カテゴリが多いほど顕著になり、「削減」という点では、２進数変換の長所です。
ダミー変換は、変数の名前がカテゴリの名前になるため、扱いやすいです。
２進数変換は、変換の対応表を参照する必要があるため、扱いにくいです。
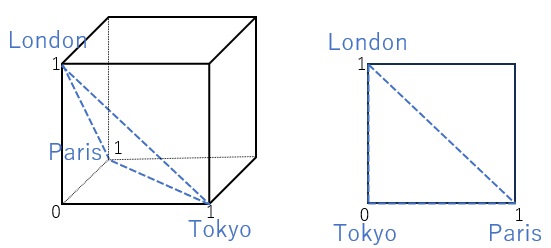
下の絵は上の絵に、２つのカテゴリの間の距離を表す線を追加しています。
左のダミー変換では、カテゴリ間の距離は、すべて正方形の対角線の長さなので、２の平方根です。
一方、２進数変換では、Tokyo-Parisが１、Tokyo-Londonが１、Paris-Londonが２の平方根です。 「距離に違いがある」という情報は、元のデータにはなかったものです。 この距離の違いは、変換する時の、処理の順番で変わってしまいます。
こうなってしまうため、 距離 を使って分析する方法を使うと、何を分析しているのかわからなくなってしまいます。
長所が効果的に働いて、短所の影響が出ないのは、記号の処理のようにして、カテゴリを扱うような時だけではないかと思います。 「コード表」といった名前で、2進数と、実際の名前の関係を定義しておいて、コンピュータは処理しますが、そういった使い道です。
データサイエンス と言われるような手法は、どれも 距離 が影響するので、不向きのようです。
Rによる2進数変換 のページがあります。
順路
次は
ファジィ理論
Tweet
