「データがあれば、 統計学 や 機械学習 で何かすごいことができる」、と思いたくなりますが、データとソフトだけではどうにもならないことは、よくあります。
文章のデータや画像のデータが、そのままではどうにもならないことは想像しやすいと思いますが、 表形式にまとまっていて、外れ値や欠損値 のない数字データだったとしても、うまく行くとは限りません。
生のデータを、 統計学 や 機械学習 で成果を出せるデータに変換する技術は、「特徴量エンジニアリング（Feature Engineering）」と呼ばれています。
音声、文章、画像などは、生のデータのままでは、機械学習で扱うことができません。 こうしたデータを表形式にまとまったデータにするための特徴量エンジニアリングは、 画像認識や音声認識 の技術として、研究されて来ています。
表形式にまとまったデータがあると、「さあ、機械学習だ。分析だ。」と、思いたくなりますが、 表形式にまとまったデータでも、特徴量エンジニアリングが必要なことはよくあります。
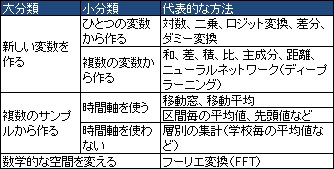
大きく分けて３種類の方法があります。 ２つ以上の種類の方法を組み合わせて、新しい特徴量を作ることもできます。
また、汎用的な特徴量として知られているものの中には、始めから２つ以上の種類に当てはまる特徴量もあります。
例えば、ベクトル量子化は、「複数のサンプルから作る」の手順の後に、「新しい変数を作る」の手順をします。
STFT（short-term Fourier transform：短時間フーリエ変換）は、３つの種類のどれにも当てはまります。
経験的には、 ドメイン知識（専門家しか知らない知識、その事象に昔から関わっている人の知識）を使って作った特徴量は、 非常に強力です。 平均値など、汎用的な方法で作った特徴量は、そうした特徴量を考えるためのヒントや補助として使う方が多いです。
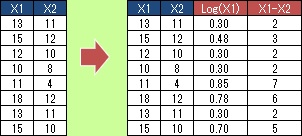
既存のデータの表に、新しい列を作る形で作成されます。
大きく分けると、ひとつの変数だけから作れるものと、２つ以上の変数を使って作るものがあります。
ひとつの変数だけから作れるものには、 対数、二乗、 標準化、 ロジット変換、 ダミー変換、 差分（ 速度データ ）、などがあります。
２つ以上の変数を使って作るものには、積（掛け算・交互作用項）、差、和、比（
足し算、割り算
）、
主成分、
独立成分、
距離、
ニューラルネットワーク
（
ディープラーニング
）などがあります。
グループ毎で 平均値や標準偏差 を計算するのは、この作り方のひとつです。 例えば、「毎日の最高温度のデータを、月毎に集計」、などです。 この集計は、 「 層別 で集計」と言われたりしますし、Excelのピボットテーブルや、BIのソフトの主要な機能にもなっています。
準周期データの分析 の中にある ２次データ（特徴量） は、ドメイン知識を活用しながら、この種類の作り方をした特徴量です。
区間ごとや、グループ変数で集計する場合、生データよりも、サンプル数（データの行数）が減ります。 かなり減ることが多いです。
例えば、 高次元を２次元に圧縮して可視化 は、データの列を減らして、データの見通しを良くしたり、計算量を減らす方法です。 複数のサンプルから作る特徴量は、データの行を減らして、データの見通しを良くしたり、計算量を減らす方法としても使えます。
移動平均
など、前後のサンプルを使って集計する方法は、新しい変数を作るような感覚で使うこともできます。
数学的な空間を変えます。 生データとは、列の名前がまったく違うものになります。
フーリエ変換
がよく知られています。
一般的に特徴量の対象になるものは、「音」、「文章」、「温度」、「点数」など、何のデータなのかを知っているデータです。 こうしたデータを「 予測 」や「 因果推論 」など様々な目的に使おうとするために、特徴量エンジニアリングが必要になっています。
ところで、特徴量エンジニアリングで扱うデータの共通点は、コンピュータで扱えるようになっている電子データである点です。 コンピュータの中でのデータの形態は、０と１の組み合わせなので、一見しても人間には何もわかりません。
実は、このページの特徴量エンジニアリングには、電子データを「音」、「文章」、「温度」、「点数」といった、 人間が何を書いているのかが理解できるデータに変換する部分は入っていません。 特徴量を自動的に作ることで有名になった ディープラーニング（深層学習） でも、この点は同じです。
電子データの根本的な部分まで扱う特徴量エンジニアリングについては、 このサイトで、いつかまとめてみたいと思っています。
「データサイエンティストのための特徴量エンジニアリング」 Soledad Galli 著 マイナビ出版 2023
特徴量エンジニアリングだけの本です。
１章：欠損値補完
２章：カテゴリ変数の変換
３章：数値変数の変換（対数、逆数、平方根、等）
４章：離散化（量的データを質的データに変換）
５章：外れ値の処理
６章：時刻データの処理
７章：スケーリング（標準化と正規化、等）
８章：新しい特徴量を作成（２つ以上の変数から作る）
９章：Featuretools（リレーショナルデータベースのような関係のあるテーブルデータから、一般的な特徴量を網羅的に作る）
10章：tsfresh（時系列データの一般的な特徴量を網羅的に作る）
11章：テキストデータの処理
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
特徴量エンジニアリングだけの本です。
１章：機械学習の手順の簡単な説明
２章：対数変換、標準化と正規化、交互作用特徴量（２つの変数の積）、など
３章：テキストデータの取り扱いとして、Bad-of-wordsで単語の使用回数を集計
４章：Bad-of-wordsのTF-IDFによる重み付け
５章：カテゴリ変数の取り扱いとして、ダミー変換など。ビンカウンティングは、単語をその単語の発生率などの統計量に変換方法。レアなカテゴリを「その他」のようにしてまとめて扱う方法の名前は、バックオフ（back-off）。
６章：主成分分析で次元削減
７章：ベクトル量子化でクラスター分析のk-means法を使って、データをグループ分けしてから、そのグループ名がある変数を、
ダミー変換などで多変数に変換する。
８章：画像データのディープラーニング（深層学習）
９章：学術論文の分析例
「事例で学ぶ 特徴量エンジニアリング」 Sinan Ozdemiri 著 オライリー・ジャパン 2023
欠損値補完、テキストデータや画像データの処理、２つ以上の変数を使って作る特徴量といったものについて、事例を通して解説しています。
手順を再利用や共用する話にもつなげています。
「Pythonではじめる機械学習 scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」 Andreas C.Muller, Sarah Guido 著 オライリー・ジャパン 2017
特徴量エンジニアリングの章があります。
ダミー変換
や、
回帰分析
の代わりに
決定木
を使って非線形の変化を解析する方法、
カーネル法
が、汎用的な方法として紹介されています。
また、専門家知識の利用として、その事象をよく知っている人にとっては常識の情報で特徴量を作る例も紹介されています。
k-means法には、
主成分分析
や
NMF
と同じように、成分分解としての使い方があるとして、ベクトル量子化を紹介。
抽出する成分の数を、次元の数よりも多くできるのが、k-means法を使った場合の特徴。
「前処理大全 データ分析のためのSQL/R/Python実践テクニック」 本橋智光 著 技術評論社 2018
数値型、カテゴリ型、日時型、文字型、位置情報型、という分け方で、それぞれの型の変換の方法をまとめています。
「AI、IoTを成功に導く データ前処理の極意」 日立産業制御ソリューションズ 著 日経BP社 2018
前処理の重要性がわかりやすく書かれていて、
「機械などの特性を確認し考慮する作業」、「入力ルールを確認する作業」など、工場のデータを扱う時の具体的な話もありますが、
具体的な話や体系的な話は、それほど豊富ではありません。
この本はタイトルや序文は「前処理」の話が中心ですが、
本文の内容は、「前処理の内容の解説」、「CRISP-DMに基ついだデータ分析のプロセスの解説」、
「機械学習のモデルの解説」、「データ分析ソフトの
KNIME
の解説」という４つ部分からできている感じです。
「Machine Learning実践の極意 機械学習システム構築の勘所をつかむ！」 Henrik Brink 他 著 インプレス 2017
特徴量エンジニアリングに２つの章を当てています。
高度な特徴エンジニアリングの章は、テキストデータ、画像データ、時系列データ。
テキストデータには
潜在意味解析（LSA）
、画像データは、エッジの抽出など。
一定間隔のデータには、一週間毎の平均値を特徴量にする事もできて、窓付き統計値(windowed statistics)と呼ばれています。
自己相関分析もこの章で紹介。
「機械学習」 Peter Flash 著 竹村彰通 監訳 朝倉書店 2017
機械学習の要素を、タスク、モデル、特徴量の３つとしています。
モデルは特徴量以上に良くはなれないので、特徴量が機械学習の成否の大部分を決定。
特徴量とは、インスタンス空間から特徴空間への写像。
特徴量の構築や選択は、行列の積の形で考えることができる。
特徴量のカテゴリーは、中心傾向の統計量（平均値など）、ばらつきの統計量（標準偏差など）、形状統計量（歪度、尖度など）
特徴量を、量的、順序、カテゴリー、ブール（二値）の４種類に分けています。
この種類分けの左側から右側へは、離散化、閾値化、順序化で行けます。
右側から左側として、キャリブレーションを挙げています。
キャリブレーションとは、確率の数字を量的変数として使うことです。
「イラストで学ぶ音声認識」 荒木雅弘 著 講談社 2015
25ms（ms = ミリ秒、1秒の千分の1）の長さのフレームを周波数分析。
フレームの端はいきなり0にならないように、減衰させる。
フレームは10msずつずらして、変化点が抜けないようにする。
ケプストラム処理をして、1番目と2番目の極大点の周波数を抽出すると、この2つの特徴量で、母音が判別できる。
「音声認識」 篠田浩一 著 講談社 2017
音声データを特徴量にするところは、上記の本よりも詳しいです。
フレームは20〜80msにするのが一般的。このフレームに対して、短時間フーリエ分析（short-time Fourier transform）をする。
フレームは10msずつずらすが、その差分も認識向上に役立つ特徴量になる。
差分ケプストラムや、デルタケプストラムと呼ばれる。
音声特徴量は、数10次元になる。
k-means
などでグループ分けして、グループ名を記憶するようにすると、1次元の特徴量となって、記憶領域の節約になる。
これをベクトル量子化と呼ばれる。
ディープラーニング
（DNN）を使って、フーリエ変換をしないで音声から特徴量を抽出する方法も開発されて来ている。
DNNの下層を
CNN
にすると、性能が高くなることもわかっている。
順路
次は
確率と確率変数の相互変換
