移動平均の考え方を使って集計されたデータの分析を、このサイトでは、「移動分析」と呼んでいます。
移動分析は、 １次データの解析 の方法になります。
移動平均は、 時系列解析 の方法として有名です。 時間軸上にあるデータについて「10個ずつ」等範囲を決めて、順次、 平均値 を計算したものです。
移動平均は、細かな変化が激しいデータの中にある、データの大きな変化を見やすくすることができます。
移動平均のように、時間軸上でデータの範囲を区切っていく方法は、他にもあります。
範囲をずらして行く感じになりますが、この範囲は「窓（Window：ウインドウ）」と呼ばれます。
音声認識 のように時系列で変化していくデータを スペクトル解析 していく時に、窓を動かす方法が使われます。
状態解析 には、モデルの劣化対策として、 時間軸に対してすべての範囲のデータでモデルを作るのではなく、 最新のデータだけ範囲を区切って使うアイディアがあります。
移動平均は昔からありますが、関係性の変化の分析方法として、「移動相関係数」と言っても良さそうな方法が注目されています。 窓を動かす方法を、 相関係数 に使います。
移動相関係数は、特徴量の変化を見る点が移動平均のアイディアと同じで、
複数の変数にまたがる窓にするのが状態解析のアイディアと同じです。
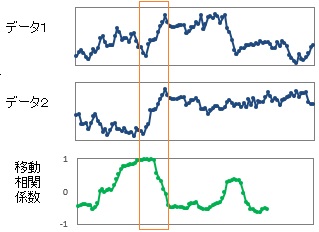
上の例の場合は、相関係数がピッタリ1になる期間があり、その期間だけは、 2つの変数が同じ動きをしている様子がわかります。
窓を動かす方法を、このサイトでは、「移動分析」と呼んでいます。
移動相関係数に限らず、時間軸上でデータを複数の範囲に区切り、それぞれの範囲で 多変量解析 をして、 多変量解析の出力値の変化を眺めると、多変量が関係する複数な変化を、シンプルな形で分析する方法になります。 0-1データの時系列解析 も、この一例です。
この方法は、一昔前のコンピューターでは無理でしたが、今は、夢のような話ではなくなっています。
移動分析のアイディアは、 異常値の判定 の方法を検討する中で、かなり研究されて来ています。
「ProVision No.78」 日本アイ・ビー・エム 2010
「スパース構造学習によるセンサー・データの変化点検出と異常解析」という題名で井手剛氏の記事があります。
時間軸上で、範囲を区切って、相関関係の
ネットワーク
構造の変化を見ていき、相関関係の変化の仕方から異常を見つける方法が紹介されています。
「異常検知と変化検知」 井手剛、杉山将 著 講談社 2015
k近傍法
やネットワークの変化、密度比を使う方法があります。
「確率と確率過程」 武田一哉 編著 オーム社 2010
窓関数として、矩形窓、ハニング窓、ハミング窓が紹介されています。
ハミング窓は、窓の端の方は、出力を小さくするもので、音声データの切り出しに使われています。
順路
次は
重ならない窓
Tweet
