スペクトル解析は、大きな波と小さな波が混ざっているようなデータの分析に使えます。
周期的な波形になっているデータは、世の中にいろいろあります。
周期性のあるデータは、 フーリエ変換 で複雑な増減を周波数（波長）毎に分解することができます。 周期的な波を、各周期での大きさに変換することによって、波の形を数字で表現します。 こうした解析は、周波数解析やスペクトル解析と言います。
フーリエ変換 の使い道は、周期的なものがわかりやすいのですが、世の中では、周期的でないデータに使われることもあります。
実際の物のすべての領域について、データを持っていない事はよくあります。 持っているデータには、範囲があります。
「範囲の中だけを正確に近似できれば良い」と考えられるケースでは、範囲を最大の周期と見なしてしまう事によって、 周期的なデータの解析方法が使えるようになります。
時間的な変化に大きな波や小さな波が混ざっている時のデータについて、 時系列解析 をしたい時にスペクトル解析が使えます。
空間的に繰り返していることに使うこともできます。 この使い方だと、例えば、表面の大きなうねりと、粗さを数値的に区別することができます。
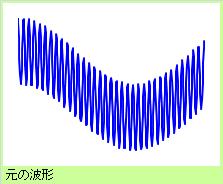
波形のデータは、いろいろな周期が混ざり合っています。 そのため、ある周期の変動を利用したり、詳しく調べたい場合は、他の周期の変動は、 ノイズ です。
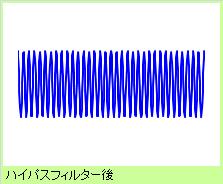
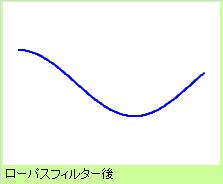
高周波を除いて、低周波を見やすくする方法を「ローパスフィルター」、 低周波を除いて、高周波を見やすくする方法を「ハイパスフィルター」、 と言います。 「ロー(low : 低い)な成分が、パスする（通る）フィルター」、という意味です。
「うねりや、ゆがみを調べたい時は、ローパスフィルター」、
「表面のザラザラ感の違いを調べたい時は、ハイパスフィルター」、と言った使い方ができます。
フィルターは、時間的な周期データにも、空間的な周期データにも使えます。
R-EDA1 では、スペクトル解析ができます。
「Time_series」
-->「One_variable（一変数）」
-->「fft(高速フーリエ変換）」と進みます。
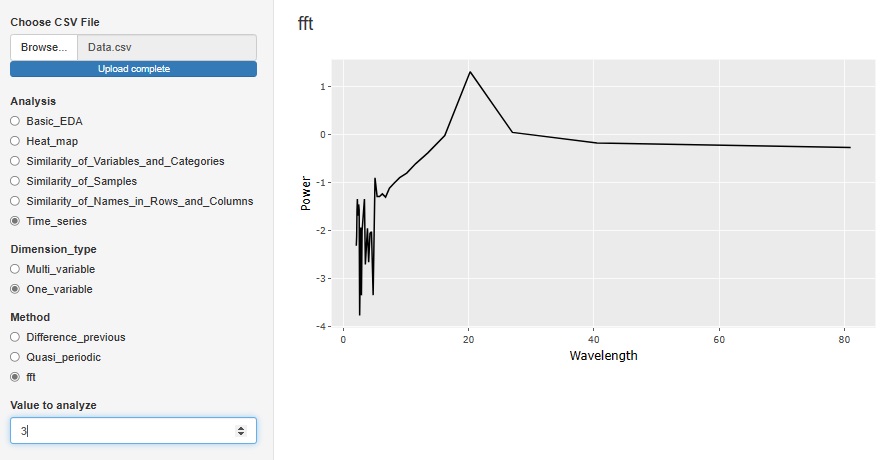
横軸は、Wavelength（波長）にしてあります。
下図の場合は、波長が20のところにピークがありますので、20行おきに周期性のあるデータであることがわかります。
「地球システムのデータ解析」 萩原幸男・糸田千鶴 著 朝倉書店 2001
２次元データの分析や、周期データの分析（フィルターの話も）を丁寧に解説している本です。
タイトルの「地球システムのデータ解析」で役に立つだけでなく、
２次元データや周期データを扱うような分野なら、幅広く参考になりそうに思いました。
この本の周期データと言うのは、
CO2サイクル・Naサイクル・地震、等です。
順路
次は
グラフフーリエ変換とスペクトルグラフ理論
