交互作用 を 重回帰分析 などで扱うための方法が交互作用項です。
交互作用項は、２つの変数の積（掛け算）で作った新しい変数です。 特徴量エンジニアリング の一種です。
「なぜ、積を作る？」、「積の意味は？」と、これだけで考え始めると、よくわからなくなりますが、これを変数として使ってみると、
面白い性質があります。
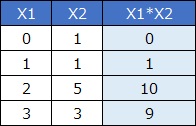
重回帰分析
では、
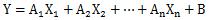
といった式を使うのが入門です。
この式で精度が高いのなら、そのデータは交互作用項のことを考えなくて良いです。
変数の重要度の分析 は、「X1とX2のどちらが、Yに影響が強いのか？」といったことを調べるのが入門ですが、 １個の変数や、複数だとしても複数の影響の足し算で済むのなら、交互作用項のことを考えなくて良いです。
交互作用項が役に立つのは、X1とX2の両方が重要で、しかも、X1とX2の単なる足し合わせではない特徴がある場合になります。
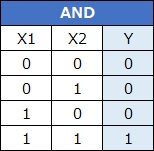
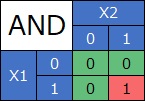
AND条件の場合、X1とX2の積（掛け算）とYの値は同じです。
ORやXORの場合、X1とX2の和や積では、Yは求まりません。
２つ以上の変数の積で作られる新しい変数は、交互作用項と呼ばれます。 変数同士の積という点は同じですが、交互作用項の性質は、ANDとはだいぶ違います。
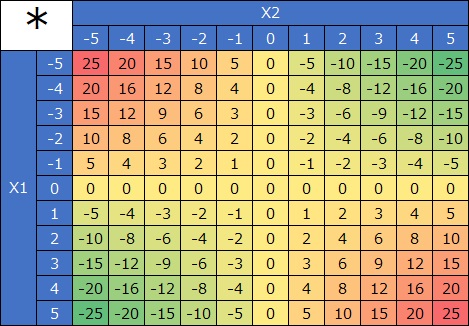
左のヒートマップは、X1とX2という変数の積です。
右の3Dのグラフは、同じデータをサーフェスプロットにしたものです。
両方の数字が増えて行くと、単なる足し算では考えられないくらい大きな数字になります。
「相乗効果」という現象が当てはまります。
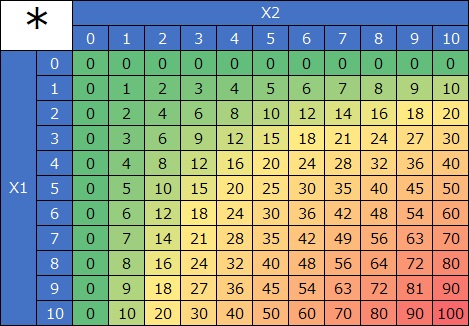
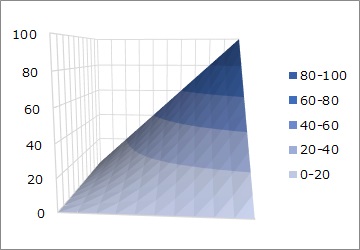
片方が０だと、もう片方がどんなに大きくてもＹが０になるのは、AND条件と同じになっています。
また、この表の左上の部分だけを切り取ると、AND条件そのものになります。
その意味で、正の数字だけというのは、AND条件の拡張と考えられます。
「Xの数字が大きければ大きいほど、Xの増え方が大きくなる」という性質だけなら、ひとつのXの２乗でも表現できますが、 交互作用項では、AND条件と似た性質が表現できます。
Xの範囲の取り方によっては、特徴が変わります。
下の場合は、X1がマイナスの時は、X2が大きければ大きいほどYが小さいのに、X2がプラスの時はX2が大きければ大きいほどYが大きくなる特徴を表します。
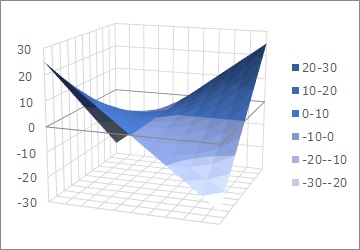
このグラフの特徴は、XOR条件と似ているので、交互作用項は、XOR条件と似ている現象が扱えると考えられます。
「Xの数字が大きければ大きいほど、Xの増え方がプラス方向。または、マイナス方向」という性質だけなら、ひとつのXの２乗でも表現できますが、 交互作用項があると、もうひとつの変数の値によって、方向が変わることを表現できます。
上記のような交互作用項の性質を重回帰分析に取り入れて、複雑なデータのモデルを作るのは、交互作用項の活用の第一歩です。 変数が１個の 単回帰分析 では、どんなに複雑なことをしても表現できなかったことが扱えるようになります。
X1、X2という変数があった時に、X1、X2の２乗や、X1*X2という交互作用項を含む 重回帰分析は、「２次モデル」と呼ばれます。
実験データの解析 で使われる 応答曲面法 はこのモデルです。
交互作用項の性質は、使い方を工夫すると、さらに応用できます。
Yが１と０で表せる場合は、 ロジスティック回帰分析 が使えます。 交互作用項があると、特徴的なデータが扱えることがあります。
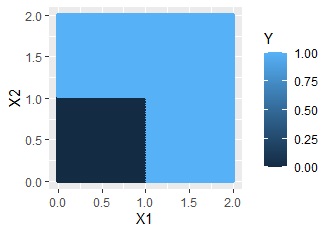
AND条件のような分布の場合です。
左が元のデータ、真ん中が交互作用項なし、右が交互作用項ありのモデルで作った予測値です。
一見すると、交互作用項ありの方が、良いように見えますが、左下の方の領域の予測値が０ではないため、必ずしもそうとは言えないです。
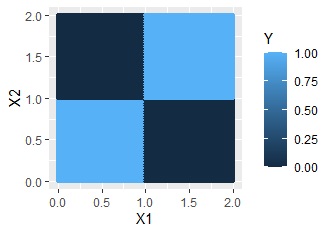
OR条件のような分布の場合です。
一見すると、交互作用項ありの方が、良いように見えますが、右上の方の領域の予測値が１ではないため、必ずしもそうとは言えないです。
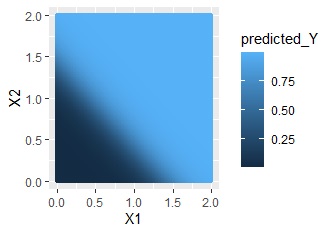
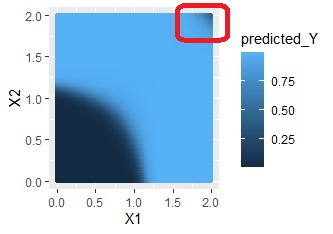
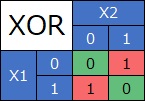
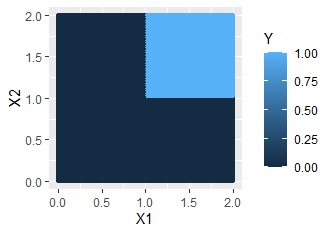
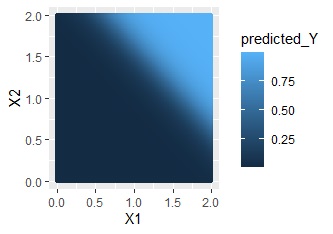
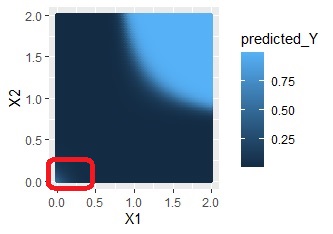
XOR条件のような分布の場合です。
交互作用項なしだと、まったくだめなのですが、交互作用ありだと、かなり精度良く予測できています。
線形混合モデル では、１と０しかない変数と、量的変数の交互作用項を作ります。 こうすると、１のサンプルだけに当てはまる回帰モデルを作れるようになります。
これだけだと、１のサンプルだけの話と変わらないのですが、 線形混合モデル では、このようにして作った複数の交互作用項の重回帰分析で、複雑なモデルを作っていきます。
線形混合モデル の応用には、 区間高次元化回帰分析 があります。
順路
次は
交互作用の分析
