区間高次元化回帰分析が向いているのは、上のようなデータです。 単純な 回帰分析 は明らかに合わなさそうですが、区間の中では、単純な回帰分析で良さそうな場合です。
区間高次元化回帰分析という名前は、筆者の造語です。 同じ方法が世の中にあれば、それに合わせるつもりですが、今のところ、そのような文献が見つからないでいます。
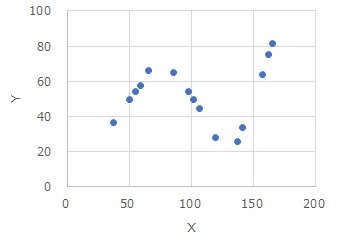
区間高次元化回帰分析が向いているのは、上のようなデータです。
単純な
回帰分析
は明らかに合わなさそうですが、区間の中では、単純な回帰分析で良さそうな場合です。
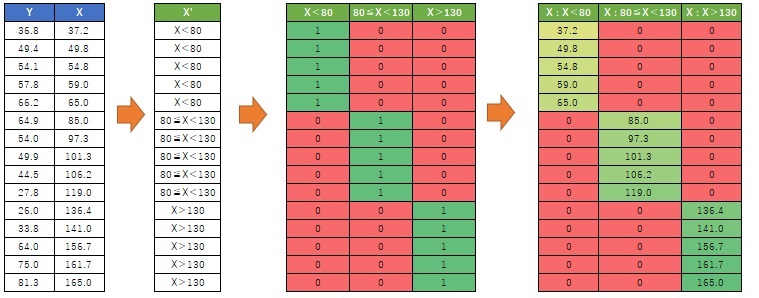
まず、説明変数を
１次元クラスタリング
で、質的変数にします。
次に、 ダミー変換 をします。
そして、ダミー変換した変数と元のXの積を作ります。 いわゆる交互作用項を作ります。
元のYに、新しく作った変数を加えたデータセットが、区間高次元化回帰分析のデータになります。
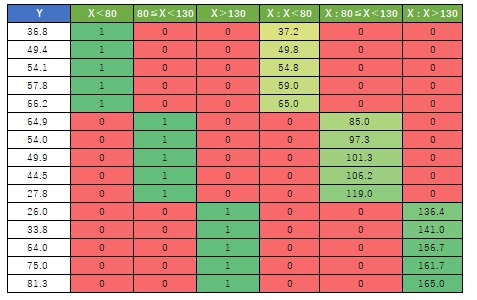
データができれば、後は、普通の重回帰分析です。
横軸を元のY、縦軸を予測値のY（Y'）にして散布図にすると、下図になります。
ほぼ一直線なので、非常に高い精度のモデルであることがわかります。
また、各区間の傾きなども、分析結果からわかります。
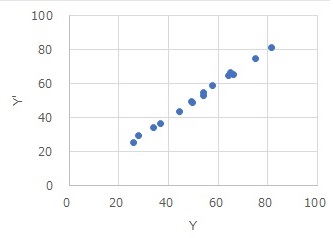
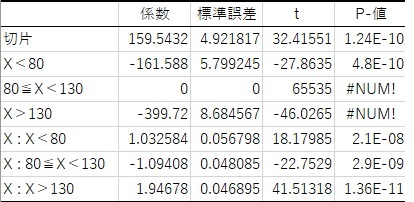
上記の例は、説明変数が１つですが、複数の場合も基本的な作業は同じです。 １変数ずつ区間高次元化の変換をして行きます。
説明変数が１つの場合は、区間で区切って、個別に単回帰分析をしても、そんなに手間ではないです。 区間高次元化回帰分析が、特に役に立つのは、説明変数が複数の時になります。
区間高次元化回帰分析は、 多変量適応的回帰スプライン 、 モデル木 、 サポートベクターマシン 、 数量化Ⅰ類 、 線形混合モデル 、 １次元クラスタリング の長所や、その長所を実現するためのアルゴリズムを、かけ合わせて作っています。 （これは、この手法を筆者が思い付いた経緯です。 世の中に同じ手法があれば、それは違う発想でできているかもしれません。）
区間高次元化回帰分析は、それらの手法と比較するとわかりやすいです。
多変量適応的回帰スプライン や モデル木 は、説明変数の空間を分けて、区間ごとに 回帰分析 をすることで、複雑なデータに単純なモデルの組合せで対応できるようにしています。
この点が、区間高次元化回帰分析も同じです。 区間ごとに単純な回帰モデルがわかる点が同じです。
サポートベクターマシン の カーネル法 では、低次元問題を高次元問題に変換することで、複雑なデータに単純なモデルで対応できるようにしています。
また、 数量化Ⅰ類 や 線形混合モデル では、質的変数を ダミー変換 しますが、これは高次元化です。 低次元問題を高次元問題に変換することで、定量的な扱いを可能にしています。
区間高次元化回帰分析も、低次元問題を高次元問題に変換してから扱います。 数量化Ⅰ類 や 線形混合モデル と同じで、高次元化は、 ダミー変換 で行います。
線形混合モデル では、質的変数を ダミー変換 した変数と、他の説明変数の交互作用項を作ります。 そうすると、質的変数のカテゴリ毎に傾きの異なるモデルが作れます。
区間高次元化回帰分析も、質的変数をダミー変換して、交互作用項を作る点は同じです。 また、これによって、質的変数のカテゴリ毎に傾きの異なるモデルを作る点も同じです。
ただ、その質的変数というのは、量的変数を １次元クラスタリング して質的変数にしたものです。 また、その質的変数から作ったダミー変数と、元の量的変数の交互作用項を作ります。 この２点は、 線形混合モデル と異なります。
上記の例は、元のデータのグラフを見ながら、Xの区間を決めています。 Rによる区間高次元化回帰分析 の例では、たまたまデータの区間を３分割したら、きれいな結果になったので、それを掲載しています。
区間高次元化回帰分析では、 １次元クラスタリング のやり方で、結果が大きく変わります。
ちなみに、 モデル木 でも似たような難しさがあるので、区間高次元化回帰分析だけの弱点ではないです。
区間高次元化回帰分析を、説明変数が複数の場合に応用しようとすると、上記のようにそれぞれの説明変数に同じ処理をします。
これと異なるアプローチとして、 クラスター分析 で、サンプルをグループ分けして、そのグループに対してダミー変数を作る方法も考えられます。 クラスター分析でグループ分けする方法は、 ベクトル量子化 と呼ばれています。
手順のイメージは下のようになります。
クラスター高次元化回帰分析は、下図のように多変数の空間にグループを作るようにしてサンプルがあり、それぞれのグループでモデルが異なる時に使えます。
クラスター高次元化回帰分析は、アプローチが モデル木 にかなり近いです。 説明変数が１つの場合は、区間高次元化回帰分析とクラスター高次元化回帰分析は、基本的に同じです。
区間高次元化回帰分析のページの例は、全部EXCELで作っています。
１次元クラスタリングとダミー変換が手作業になりますが、やろうと思えば、EXCELでもできるのが、区間高次元化回帰分析の良いところです。
Rの実施例は、 Rによる区間高次元化回帰分析 にあります。 クラスター高次元化回帰分析の例もあります。
下記の２冊の文献は、 ラベル分類（目的変数が質的変数）の方法として、説明変数にクラスター分析を使う方法を紹介しています。 交互作用項を作る話は、出て来ません。 上記のクラスター高次元化回帰分析は、目的変数が量的変数の場合です。 回帰問題の場合は、交互作用項を作ると、精度がかなり良くなって実用的な感じになります。
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
クラスター分析のk-means法を使って、データをグループ分けしてから、そのグループ名がある変数を、
ダミー変換などで多変数に変換します。
これを
ロジスティック回帰分析
の説明変数として使っています。
「Pythonではじめる機械学習 scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」 Andreas C.Muller, Sarah Guido 著 オライリー・ジャパン 2017
k-means法の説明から、ベクトル量子化の説明になります。
その後で、クラスターを作ってから、１と０の変数を作ると、複雑な分布を線形モデルで分離できる、という方法が紹介されています。
順路
次は
比例分散の線形混合モデル
Tweet
