スプライン

一般的な回帰分析は、単純な数式を仮定して、一番当てはまりが良くなるように、数式のパラメータ（係数）を求めようとします。

スプラインは、どちらかと言えば、データの当てはまりが良いことを優先して、複雑な数式を求めます。

スプライン補間

スプライン補間は、全部のサンプルを滑らかにつなぐ曲線を描く方法です。下の図は、Excelで作っています。
spline

平滑化スプラインは、スプライン補間と回帰分析の間にある方法です。パラメータの設定の仕方で、どちらかと同じ結果になるようにもできます。

多変量適応的回帰スプライン（Multivariate Adaptive Regression Splines：MARS）は、「スプライン」の仲間ですが、上記の2種類と違って、数式が出力されます。

データの並び方に単純なルールがあるのなら、単純な数式になります。一般的な回帰分析と、上記の2種類の中間にあるような方法です。

多変量適応的回帰スプラインでは、ヒンジ関数（Hinge function）の足し合わせた数式に当てはまるようにします。ヒンジ関数には、区間で回帰分析をする要素が入っているので、回帰分析とスプラインの両方の特徴を持つ方法になっています。

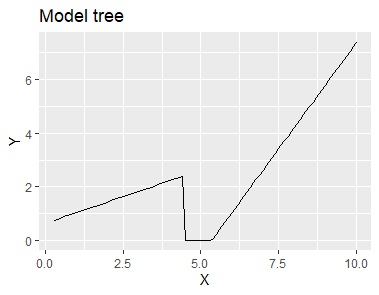
モデル木は、データを区間で区切って、区間ごとに一般的な回帰分析をした結果が出せます。

多変量適応的回帰スプラインも、区間で回帰分析をする要素が入っている点が同じです。

両者の違いですが、モデル木では、その区間の中のデータだけで数式を出すのに対して、多変量適応的回帰スプラインでは、全部のデータに対して数式の当てはまりを見ている点になります。

ディープラーニング（深層学習）では、活性化関数としてReLU関数（ランプ関数）を使うことがあります。

多変量適応的回帰スプラインで使うヒンジ関数と、ReLU関数はとても似ています。ヒンジ関数で、原点が折れ曲がりの点に限定した場合が、ReLU関数になっています。

そう考えると、「多変量適応的回帰スプラインは、ディープラーニングで中間層が一層で、活性化関数をReLUにした場合」と考えても良さそうです。

左から順に、データ、スプライン補間、平滑化スプライン、多変量適応的回帰スプライン、モデル木です。
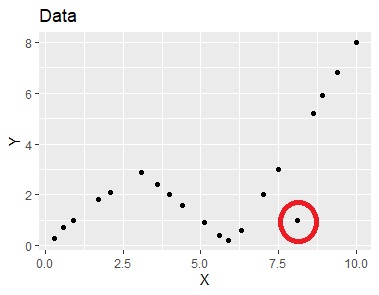
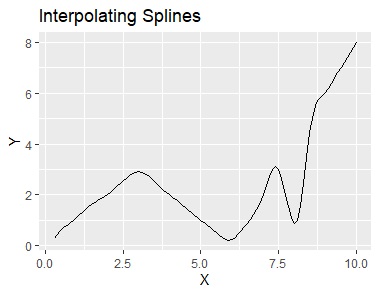
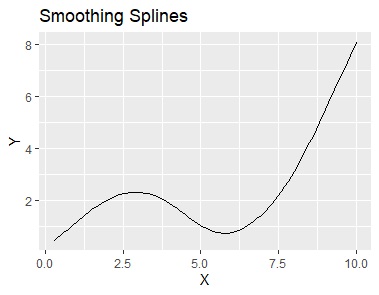
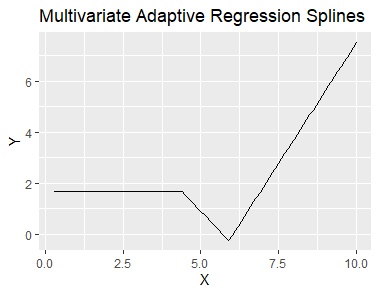
spline spline spline spline spline

Rの実施例は、 Rによるスプラインにあります。

「スプライン関数入門　情報処理の新しい手法」　桜井明　編著　東京電機大学出版局　1981
スプラインの数学的な基礎を解説している本です。CADなどへの応用の話もあります。
複雑な関数をシンプルに近似する有力な方法として、区分多項式を紹介しています。平滑化スプラインもあります。

「平滑化スプラインと加法モデル」　馬場真哉　著　2017
Rによる実施例も含めて、具体的に解説されています。
https://logics-of-blue.com/%E5%B9%B3%E6%BB%91%E5%8C%96%E3%82%B9%E3%83%97%E3%83%A9%E3%82%A4%E3%83%B3%E3%81%A8%E5%8A%A0%E6%B3%95%E3%83%A2%E3%83%87%E3%83%AB/

「多変量適応的回帰スプライン(MARS)をPythonで試してみる」　キヨシ　著　2020
数少ない日本語の解説です。Pythonの実施例があります。
https://yolo-kiyoshi.com/2020/12/01/post-2430/

「Multivariate adaptive regression spline」
Wikipediaの英語版です。コンパクトに解説されています。
https://en.wikipedia.org/wiki/Multivariate_adaptive_regression_spline

「活性化関数」
Wikipediaです。ニューラルネットワークにReLU関数を使う発想は、線形補間から来ていることが書かれていました。
https://ja.wikipedia.org/wiki/%E6%B4%BB%E6%80%A7%E5%8C%96%E9%96%A2%E6%95%B0