トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

モデル木

モデル木（Model tree）は、決定木（回帰木）と回帰分析を混ぜたような手法になっています。層別サンプリングの回帰分析を、自動で発見的に実行する方法になっています。

一般的な決定木では、データ全体の部分的な特徴を見ることができますが、数式で考察することができません。回帰分析は、データの全体をひとつの数式で表せる時は良いのですが、そうでない時は、うまく行きません。モデル木は、両者の弱点を補完し合う方法になっています。

一般的な回帰木とモデル木の違い

「一般的な回帰木」というのは、rpartやランダムフォレストで、Yが量的変数の時に実行される方法のことを、ここでは指しています。

一般的な回帰木の弱点

一般的に回帰木として知られている方法は、「層別による分散分析」とも言える方法になっています。データを層別（区分）してグループを作り、グループの平均値に差があるかどうかを見て行きます。

グループの違いを見るので、「Yの高い方と低い方の違い」といったことはわかります。しかし、同じグループ内は、予測値が同じになるため、予測値の精度があまりよくありません。グループを細かくすると、予測値の精度は改善しますが、複雑過ぎて考察のできないモデルになります。

モデル木の違い

モデル木は、同じグループの中で回帰分析をします。これによって、グループの中での値の違いも表現できるようになります。

そのため、グループを細かくしなくても、予測値の精度が一般的な回帰木よりも、良くなります。

一般的な回帰木は、「回帰」と付いていますが、いわゆる回帰分析のように、
Y = a*X + b
のような式は使いません。

一方、モデル木では、各グループの中で、
Y = a*X + b
のような式を当てはめて行きます。

モデル木の実施例

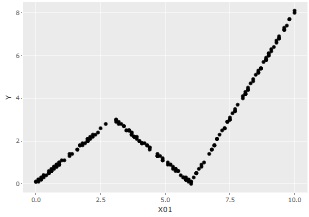
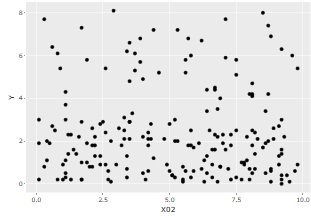
model tree
上のように、X01、X02、Yという３つの変数があり、YとX01には、関係のようなものがあるものの、YとX02は無関係のデータがあったとします。

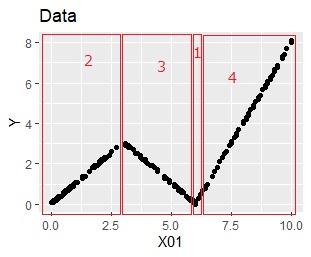
これをモデル木で分析すると、モデルは下記になります。３つのグループで表現できそうですが、４つが抽出されています。４つのルールがそれぞれシンプルな回帰分析の結果になっています。
model tree

４つのルールを元のデータと見比べると、元のデータを区間の中で成り立っているシンプルな回帰式が、それぞれのルールと対応しています。
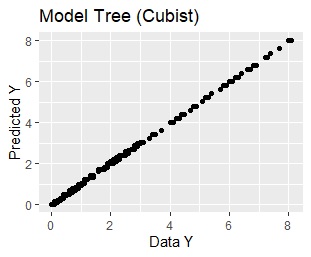
model tree

このモデルを使って、予測値を出します。下のグラフは、横軸が元のデータのYで、縦軸が予測値のYですきれいに一直線状に並んでいますので、非常に高い予測ができていることがわかります。
model tree

他の手法との違い

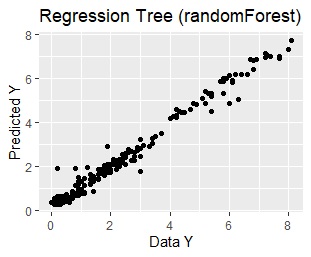
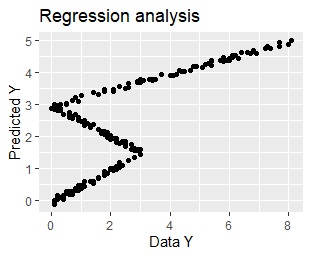
同じデータを使った結果です。左からrpartの回帰木、ランダムフォレストの回帰木、重回帰分析になります。
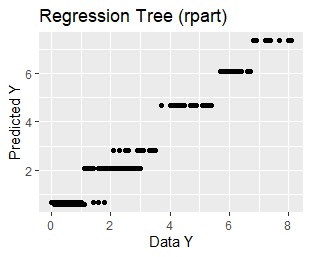
model tree

rpartは、同じグループの中では、予測値が同じになることがグラフからもわかります。

ランダムフォレストは、高い精度は出せているように見えますが、モデルが複雑過ぎて、 Yと、X01やX02の関係が考察できません。モデルを使って、対策を考えることにもつながらないです。

重回帰分析は、X01の区間によって、適した式が異なることを表現できないので、実用には、ほど遠いような予測値になっています。

ソフト

R

Rによるモデル木のページがあります。

R-EDA1

R-EDA1 でもできます。
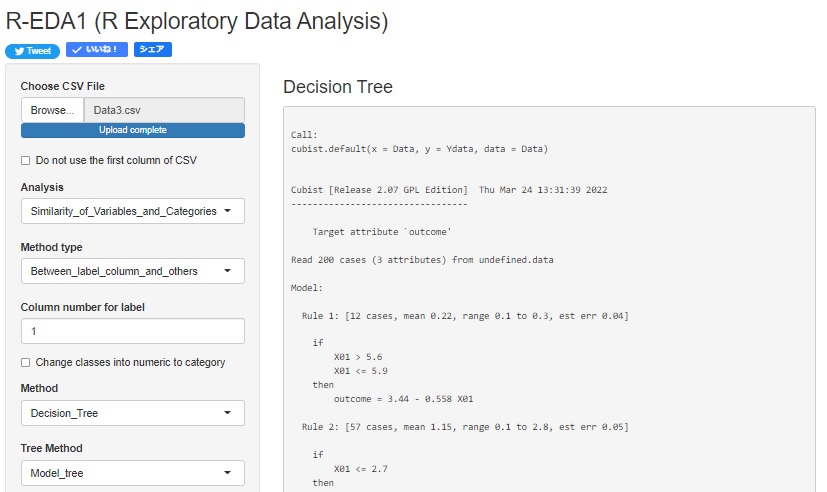
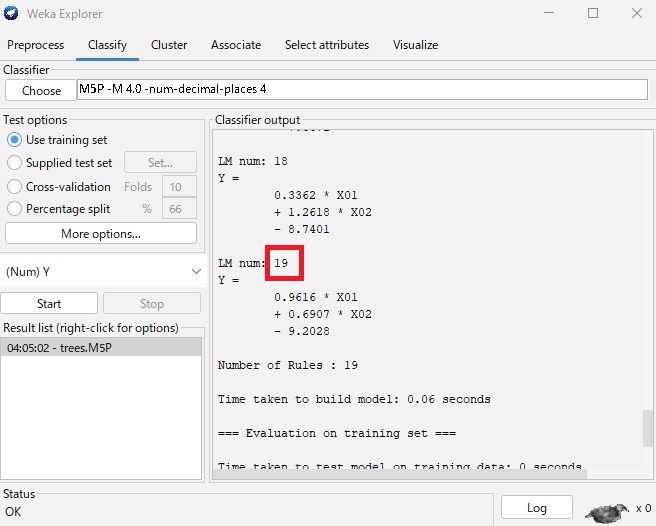
model tree

Weka

Wekaはtreesの中にあるM5Pがモデル木です。このページの上の例は、RのCubistで作っていて、ルールが４つ出て来るのですが、同じデータをWekaのM5Pにすると、19もルールが出て来て、モデル木の特徴の「シンプルなモデル」という風になって来ません。
model tree

参考文献

「Rによる機械学習」　Brett Lantz　著　翔泳社　2021
第6章で、モデル木は、決定木と回帰木の長所を持つものとして紹介しています。

WEKAと樹木モデル
金明哲先生のページです。 WEKAの決定木の中に、M5Pという方法があり、「線形回帰式を葉に持つモデル木」として紹介されています。
https://www1.doshisha.ac.jp/~mjin/R/Chap_20/20.html

RWeka::M5Pに代わるモデリング関数
RWekaを使うと、WekaのM5PがRでできるのですが、Wekaで実行した結果と異なるそうです。ここでは、Cubistというアルゴリズムを、M5Pを拡張した方法として紹介しています。
https://k-metrics.netlify.app/post/2019-11/rweka-m5p/

線形回帰モデルとモデル木の比較
線形回帰と、Cubistのモデル木の比較があります。
https://k-metrics.netlify.app/post/2019-11/cubist/

「マテリアルズ・インフォマティクス　材料開発のための機械学習超入門」　岩崎悠真　著　日刊工業新聞社　2019
物性値をYとして、物質の構造を表す多変量をXとした時の、分析方法の本になっています。
モデル解釈性、予測性能、スパース性がバランス良く両立した方法として、 FAB/HMEsという方法を紹介しています。この本の中で、FAB/HMEsを「モデル木」として紹介していないのですが、説明を読む限りでは、この方法はモデル木の一種と考えれば良いようです。

順路次はカテゴリの類似度の分析