ベクトル量子化回帰分析という名前は、筆者の造語です。 同じ方法が世の中にあれば、それに合わせるつもりですが、今のところ、そのような文献が見つからないでいます。
区間高次元化回帰分析 を、説明変数が複数の場合に応用しようとすると、それぞれの説明変数に同じ処理をします。
これと異なるアプローチとして、 クラスター分析 で、サンプルをグループ分けして、そのグループに対してダミー変数を作る方法も考えられます。 クラスター分析でグループ分けする方法は、 ベクトル量子化 と呼ばれています。
手順のイメージは下のようになります。
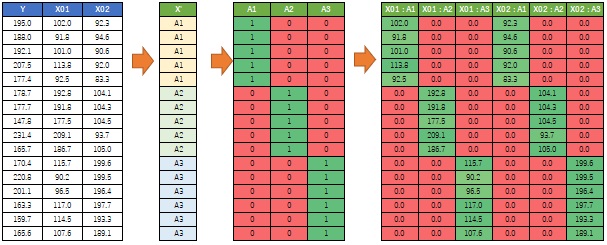
ベクトル量子化回帰分析は、下図のように多変数の空間にグループを作るようにしてサンプルがあり、それぞれのグループでモデルが異なる時に使えます。
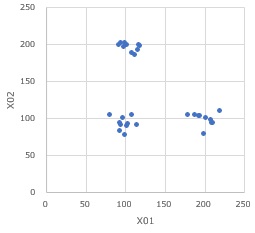
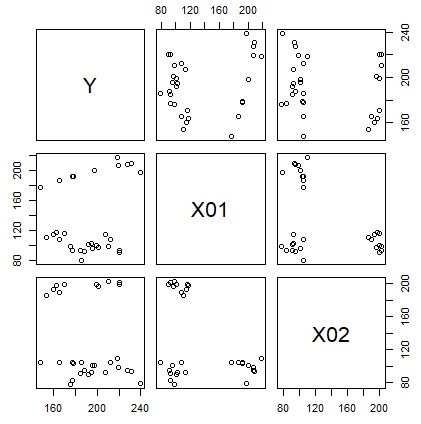
ベクトル量子化回帰分析は、アプローチが モデル木 にかなり近いです。 説明変数が１つの場合は、区間高次元化回帰分析とベクトル量子化回帰分析は、基本的に同じです。
Rの実施例は、 Rによるベクトル量子化回帰分析 にあります。
下記の２冊の文献は、 ラベル分類（目的変数が質的変数）の方法として、説明変数にクラスター分析を使う方法を紹介しています。 交互作用項を作る話は、出て来ません。 上記のベクトル量子化回帰分析は、目的変数が量的変数の場合です。 回帰問題の場合は、交互作用項を作ると、精度がかなり良くなって実用的な感じになります。
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
クラスター分析のk-means法を使って、データをグループ分けしてから、そのグループ名がある変数を、
ダミー変換などで多変数に変換します。
これを
ロジスティック回帰分析
の説明変数として使っています。
「Pythonではじめる機械学習 scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」 Andreas C.Muller, Sarah Guido 著 オライリー・ジャパン 2017
k-means法の説明から、ベクトル量子化の説明になります。
その後で、クラスターを作ってから、１と０の変数を作ると、複雑な分布を線形モデルで分離できる、という方法が紹介されています。
順路
次は
比例分散の線形混合モデル
