実験計画法 には、計画する段階と、 実験で得られたデータを解析する段階があります。 実験後のデータ解析は、それぞれの分野に合った手順が考案されています。
きちんと計画されて収集したデータを使うと、精度の高い解析をすることができます。
分散分析は、水準を質的データとして扱います。 回帰分析は、水準を量的データとして扱います。
実験データの分析では、 交互作用の分析 をするのが一般的です。 交互作用項 は、特別なものではないです。
多元配置分散分析 は、現象の関係の深い因子を抽出するために使われます。
「分散分析」という名前ですが、平均値を評価するための方法です。
実験には、 測定の精度、 サンプリングのタイミングの違い、 実験の再現性、 水準の違い、 採用した因子、 といったものがありますが、それらはすべて「ばらつき」として見えます。
例えば、同じ実験を2回行って、測定結果が2個あるとすると、 実験の再現性、サンプリングのタイミングの違い、測定の精度が混ざっています。 測定の精度を分離するには、測定だけを繰り返した場合のばらつきのデータが必要です。
測定精度のばらつきを推定するために、測定の繰り返しのデータがあれば、 分散分析表を、ばらつきの分離に使うことができます。
ただし、分散分析表でできるばらつきの分離は、因子の違いや、測定精度についてです。 分散分析は、等分散を仮定しているので、各水準特有のばらつきを、分散分析表で推定することはできません。 水準特有のばらつきを評価するには、 品質工学 から提案されている 直交表の外側配置 を使います。
重回帰分析 は、実験の結果を「法則」として定式化したり、 最大値や最小値を見つけるために使われます。
二次式の回帰分析を使う場合は、 応答曲面法 と言われることもあります。
回帰分析の注意点に 多重共線性 がありますが、 直交表を使って取ったデータは、直交しているため、多重共線性の心配をする必要がありません。
要因効果図は、 因子毎・水準毎の集計値のグラフです。 実験の生データのばらつきは見えなくなるのですが、実験の結果をわかりやすくまとめるのに使われます。
要因効果図を使うと、線の様子で交互作用の有無が判断できます。
水準で層別して、平均値を結んだ線を描いた時に、
交互作用がない場合は、だいたい平行になります。
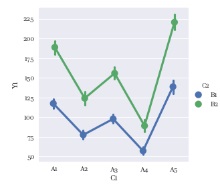
XORの交互作用がある時は、交差したところが出て来ます。
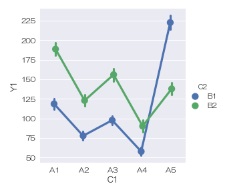
実験では、 「なぜ、その条件が最適なのか？」という理由の考察が大切な事があります。 結果がわかってから理由を考えると、 考えやすいです。 （その場しのぎの理由で、自己満足して終わってしまうこともありますが、、、）
実験の定量的な結果ばかりに気をとられると、 定性的な結果を忘れがちです。 普通、実験は「測定」だけが目的ではなく、「どうなるか」を知るのも目的なので、 数字にこだわり過ぎない方が良いです。
悪いケースを想定するなら、 「実験した時には知らなかった因子によって、後になって実験結果がひっくり返ることがない。」とは、 普通は言えないです。 実験をする時には、こういうことも承知した方が良いと思います。 ひっくり返った時の対策を早くするためには、実験した時の考察が大事だと思います。
順路
次は
多元配置分散分析
