次は
混合系の直交表
外側配置は、 品質工学の直交表 の特徴のひとつです。 二段階設計 、 誤差因子 、 信号因子 といったアイディアを具体的に使うための方法になっています。
以下は、因子が２つ、それぞれの因子について水準が２つの実験計画法を例にして、外側配置を説明しています。 混合系の直交表 等、他の表を使ったとしても、やり方は同じです。
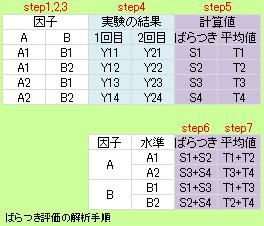
「ばらつき評価の解析手順」という表は、ばらつきの尺度を計算して評価するための、基本になるものです。 この場合は、単純に同じ実験を２回繰り返すことを想定しています。
例えば、A1水準の実験は、B1とB2について2回実施されているので、 A1水準のばらつきは、Y11とY12から求まるようにも見えなくもありません。 そうだとすれば、各実験は1回でも、ばらつきが計算できるように見えます。
しかし、この場合ですと、Y11とY12の違いが、A1を繰り返すことによるばらつきなのか、 B1とB2の水準を変えたことによる差なのかを、区別できません。
A1のばらつきと判断できるのは、因子Bが実験結果に影響しないことが、あらかじめわかっている場合です。 また、B1とB2の差と判断できるのは、A1の繰り返しのばらつきが非常に小さいことが、あらかじめわかっている場合です。 （ちなみに、一般的な 実験計画法 では、B1とB2の差と解釈してしまうことが多いです。）
各実験を2回以上していれば、ばらつきの原因を区別できるようになります。
外側配置の形で書いていなくても、 同じ実験を複数回実施しているとみなせる実験の場合は、ばらつきの尺度を計算することができますが、 どのデータを使って計算したのかがわかりにくいです。 外側配置は、その点で便利です。
Step5の「ばらつき」の尺度ですが、 品質工学 からは、 SN比 が提案されています。
一般的には、ばらつきと言えば、 標準偏差 を指すことが多いですが、 Step6でばらつきの尺度の足し算をする事を考えると、 誤差の伝播 のところにもありますが、 標準偏差は不適切な尺度ということになります。
※１ 「SN比は、加法性を考えて作られている」、と言われていますが、SN比にもいろいろあるので、 すべてのSN比がそうであるのかは疑問があります。
※２ ただ、現実のデータでは、解析の対象となるデータに正規性がなかったり、 大づかみな情報しかわからなかったりするので、 標準偏差を使うのは絶対にダメ、という事はないと思っています。
ここでは、計算の流れをわかりやすくするために足し算で書きましたが、 n数で割って、ばらつきの尺度の平均値や、平均値の平均値を計算する方が、物理量としてはわかりやすいです。
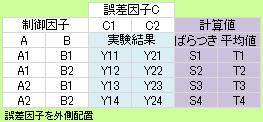
誤差因子 によって外乱をわざと発生させて、 外乱の影響がある時のばらつきを評価することにも、外側配置は使われます。
「誤差因子を外側配置」の表は、 単純に２回繰り返すのではなく、誤差因子の水準を変えることを想定しています。 解析の手順は、「ばらつき評価の解析手順」という表と、同じになります。
誤差因子の水準を設定しているので、同じ実験を2回していないです。 「誤差因子によって、ばらつきが、より強調されて出るようにした。」、と考えているので、 同じ実験を2回していなくても、ばらつきを評価できています。 （「誤差因子で強調された」とみなすことができない場合は、使えない方法です。）
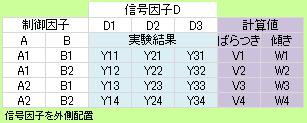
もうひとつの使い方が、 信号因子 を評価するための外側配置です。 「信号因子を外側配置」の表は、信号因子が３水準の場合を想定しています。
図の見た目は誤差因子の場合に１列増えているだけです。 しかし、XとYの２次元的な関係を見るので、 解析の計算をする時に、信号因子の水準の値を使う点が異なります。 例えば、V1は、（D1、Y11）、（D2、Y21）、（D3、Y31）を使って、 相関係数 等を、計算します。
二次元的なばらつきを評価するためには、信号因子は３水準以上が必要です。
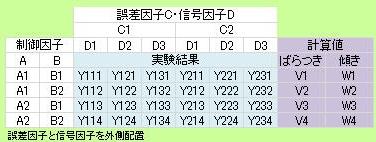
誤差因子のことも考えた信号因子を使う実験は、 「誤差因子と信号因子を外側配置」の表になります。 文献等で 動特性 を学ぶと、いきなりこの表が登場することが多いと思います。
特性とSN比の関係 のページに書いた「動特性のSN比」は、 信号因子だけを配置した場合の計算式になります。 多くの文献では、もっと複雑な式が書かれていますが、 その式は、誤差因子と信号因子の両方を配置した場合の計算式になります。
順路
次は
混合系の直交表
