因果推論 で 定量的な仮説の探索 などの時では、「目的変数に一番影響している変数は？二番目は？」という分析に進みたいことがあります。 「診断」や「項目診断」と呼ばれる事もあります。
また、 変数の選択 でも変数の重要度は、重要な情報になります。
なお、このページは、 重回帰分析 の子ページですが、重回帰分析以外でも、基本的な考え方は同じです。
重回帰分析 のページにある係数評価や、変数毎のp値の評価は、変数の重要度の分析の一種です。
「回帰式の中の、変数の重要度の分析」は、回帰式ができた後に、その回帰式に対してできる方法です。 回帰式ができる前に、「この変数は、回帰式にいれるべきか？」、「この変数は、目的変数に影響が大きいと言えそうか？」ということを調べる方法は他にもあります。
アンサンブル学習による方法も、実験計画法による方法も、すべての変数を使わない回帰式（モデル）の様々なパターンを試しに作ってみて、それぞれの評価をします。 こうすると、他の変数との 多重共線性 の影響などによって、すべての変数を使った回帰式では、重要ではないという評価になってしまっているものの、実は重要な変数を見つけることができます。
アンサンブル学習 は、精度の高いモデルを作る方法として解説されていることが多いですが、変数の重要度の分析の方法として使われることもあります。
決定木 のモデルでは、 ランダムフォレスト がアンサンブル学習を利用して、変数の重要度の分析になっています。
実験計画法 と 実験データの解析 をセットにした方法は、変数の重要度の分析としては、おそらく一番古い方法です。
品質工学 の MTシステム では、 実験計画法 を応用する方法が考案されています。
２水準系の直交表は、０と１の２値でできていますが、 この０と１について、「０ ＝ なし（その説明変数はモデル式に入れない）」と「１ ＝ あり（その説明変数はモデル式に入れる）」と考えます。
実験計画法では、条件のいろいろな組み合わせを順に実験して行きますが、 同様に、説明変数を選択した状態のいろいろな組み合わせについて、順番にモデル式の良さを計算します。
計算してから、要因効果図を描くと、影響の大きな説明変数を見つけることができます。
人工知能（AI） のモデルでは、そのモデルの中での変数の重要度がわかることは、 AIの説明可能性・解釈可能性 を高めることになります。
AIの説明可能性・解釈可能性 の方法としては、従来からの変数の重要度の分析の方法に加えて、新しい方法も登場しています。
ちなみに、 AIの説明可能性・解釈可能性 の分野では、あるモデルについての変数の重要度だけでなく、 「あるサンプルについて、そのサンプルではどの変数が重要なのか？」ということを調べる方法もあります。
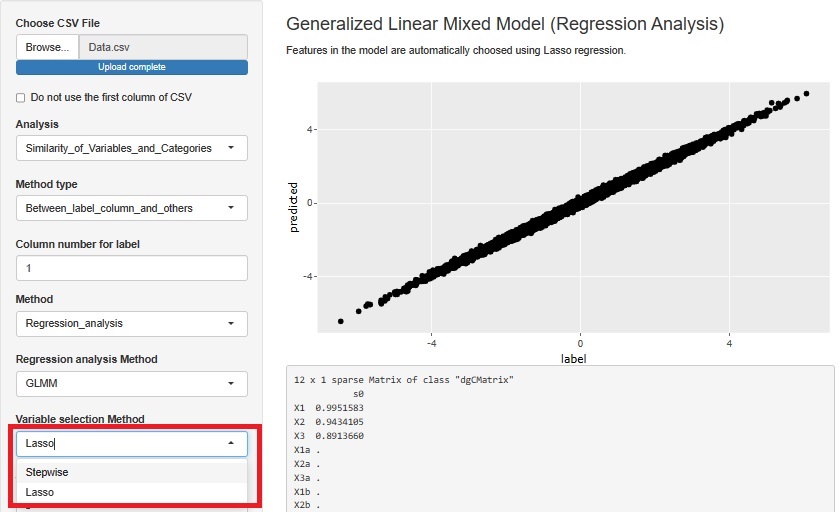
Rによる変数の選択があります。
R-EDA1
では、ステップワイズ法（変数増減法）とLasso回帰が選べるようになっています。
順路
次は
変数の重要度の過少評価
