変数の重要度の分析 のRでの実施例です。
Rによる一般化線形混合モデル のページと重複する内容もありますが、このページは、変数の選択 の機能を中心にまとめています。
下記の例は、 重回帰分析 のものです。 一般化線形モデル なので、 ロジスティック回帰分析 などもできます。
一般的に「ステップワイズ法」と言われる時は、変数増減法のことが多いです。
library(MASS)
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data1 <- read.csv("Data.csv", header=T) # データを読み込み
gm <- step(glm(Y~., data=Data1, family= gaussian(link = "identity")),criteria = "AIC",direction = "both") # 変数増減法
summary(gm) # 結果の出力
「direction = "both"」のところは、"both"（変数増減法）, "backward"（変数減少法,） "forward"（変数増加法）が選べます。 「direction = "both"」を省略すると、デフォルトの"both"になります。
「criteria = "AIC"」のところは、"AIC", "AICc", "AICb1", "AICb2", "BIC", "KIC", "KICc", "KICb1", "KICb2"と、いろいろ選べます。 「criteria = "AIC"」を省略すると、デフォルトの"AIC"になります。
変数の選択
のページと同じデータの結果が下記になります。
ほぼ正確に係数が計算されています。
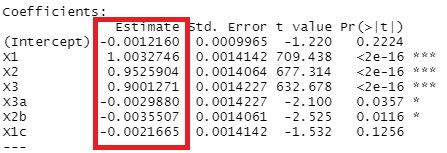
glmnetのパッケージには、説明変数を標準化してから実行する機能がデフォルトで入っています。 そのため、求まる係数は標準偏回帰係数となり、これを使っては、変数の影響度を評価できます。
library(glmnet)
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data1 <- read.csv("Data.csv", header=T) # データを読み込み
Y <- Data1$Y # Yの列を別に作っておく
Data1$Y <- NULL # Yの列を消す
lasso.cv <- cv.glmnet(x = as.matrix(Data1), y = Y, family = "gaussian", alpha = 1) # ラッソ回帰のλを見つける
lasso <- glmnet(x = as.matrix(Data1), y = Y, family = "gaussian", alpha = 1,lambda = lasso.cv$lambda.min) # ラッソ回帰
lasso$beta# 結果の出力
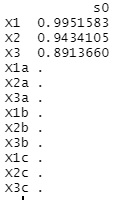
出力されるのは、回帰式の係数です。
「family = "gaussian"」のところは、"gaussian", "binomial", "poisson", "multinomial", "cox", "mgaussian"と、いろいろ選べます。上記のglm関数と似ています。 "gaussian"の場合は、重回帰分析です。
データは、上記のステップワイズ法と同じです。
X1、X2、X3以外は0になり、３つの変数がきれいに抽出されています。
R Documentation
step関数の詳細の説明があります。
https://search.r-project.org/R/refmans/stats/html/step.html
biostatistics
ラッソ回帰のλの推定のところが参考になりました。
https://stats.biopapyrus.jp/sparse-modeling/glmnet.html
CRAN
glmnetのマニュアルです。
https://cran.r-project.org/web/packages/glmnet/glmnet.pdf
