現実と統計モデルとのギャップ や 回帰分析 のページにも書きましたが、重回帰分析がうまく行かないことは、多々あります。 このページは、ちょっと工夫すれば、うまく行く例です。
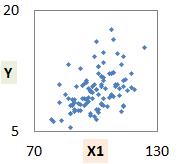
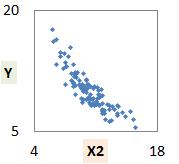
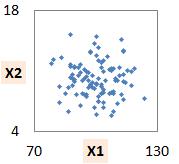
Y、X1、X2という３つの変数があって、 ２つずつの組み合わせの関係は、図のようになっていたとします。 Yは結果を表していて、X1とX2は原因と考えているとします。
図は、「YとX1は少し比例関係があるかも」、「YとX2は反比例のような感じ」、「X1とX2は無相関」、と言ったように見えます。
原因になっていると考えられる変数が複数あって、結果の変数がある時は、 多変量解析 を勉強した事があると、 「まず、 重回帰分析 をしてみよう。」 、という風に進む事が多いと思います。
重回帰分析では、
Y = a1 * X1 + a2 * X2 + b
という式（モデル）で変数の関係を表現します。
このページでは、このようなモデルを「足し算モデル」と呼んでいます。
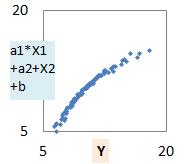
足し算モデルの場合、Yとモデルで推定した値の関係は、下図のようになります。
ななめ45度の一直線上に点が並ぶと、モデルが完璧という意味になるのですが、一直線にはなっていません。
「YとX2は反比例のような感じ」という点に着目して、
X1 / X2
という数字を計算することにします。
足し算モデルの時と同じように、X1 / X2 と Y の関係を散布図で表すと、下図のようになります。 こうすると、ほぼ一直線になりました。
（実のところ、このページのデータは X1 / X2 を計算して、それを少しばらつかせてYを作っているので、
このページのデータについては、
X1 / X2
が正解です。）
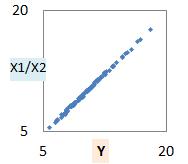
会計の分析 、 環境影響の尺度 、 自然環境 の理論などなど、様々な分野で、２つの種類の数字（変数）の割り算で作られた数字は、よく使われます。 「○○指数」などと呼ばれることもあります。
割り算でできている数字について、 因果関係の分析 をしようとすると、このページのような事が起きます。
「答えがわかっていたから割り算モデルが出て来たが、わかっていなかったら、割り算モデルを思い付くのは難しいのではないか？」、 という疑問があるかもしれません。
確かにそうだと思います。
ただ、 X1とX2の単位が違う時には、足し算モデルは 次元解析 の観点で見ると、不自然なモデルです。 Yの次元（単位）にもよりますが、こういう時には、X1 / X2 の方が、真実に近いことはあり得ます。
「YとX2は反比例のような感じ」という点に着目するのなら、
Y = a1 * X1 + a2 / X2 + b
という式（モデル）での表現も考えられます。
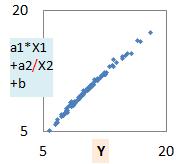
このモデルとYの関係を散布図で表すと、下図のようになります。
割り算モデルほどではないですが、最初の足し算モデルよりは、かなり改善しました。
このページの例では、「割り算モデルが正解」になりますが、 「推定値は、だいたい合っていれば良い」、という程度が分析目的でしたら、どのモデルでも大差ありません。 因果関係の分析 をするにしても、足し算モデルの結果は参考になります。
こうしたことから、重回帰分析は ロバストな解析 と言えます。
上記は、 「X1が大きいほど、Yが大きくなる。 また、X2が大きいほど、Yが小さくなる。」という関係を表す時に、 足し算モデルと割り算モデルがだいたい同じ結果になる話でした。
両方のモデルが同じになるのは、X1とX2の数字が正の値（プラスの数字）の時です。 負の値（マイナスの数字）が入っていると、同じ結果にならなくなります。
正の値しかないデータを、何かの規則で、正と負の両方がに分かれるように変換したり、 逆に、正と負の両方が混ざっているデータを、正だけになるように変換する事と、 足し算モデルや割り算モデルの性質を、うまく組み合わせる事で、分析の見通しを良くする手が考えられます。 （筆者自身は、まだ試した事がありませんが）
このページのデータは、 サンプルファイル で作りました。
順路
次は
確率論モデルと決定論モデル
