一般的に「予測」と言えば、いろいろな情報を使って、確からしい予測をしようとします。
一方、時系列近傍法は、自分の過去の情報だけで、予測をする方法です。 これが可能なケースなら、ぜひ使いたい方法になります。
「時系列近傍法」という名前なので、何か特別な予測の方法のように見えるかもしれませんが、 例えば、「最近３日間は、雨が降っていないから、今日の昼は晴れだろう。」 、という予測は、時系列近傍法の一種です。
多くの時系列分析の本では、「ARMA」、「ARIMA」、「SARIMA」といった名前の方法を中心にして解説しています。 このサイトでは、その系統の方法を、他の方法と区別するために、「時系列近傍法」という名前で呼ぶことにしています。
「時系列」がない「 近傍法 」というのは、 データマイニング で、もっともシンプルな方法として知られています。 近傍法では、近くのデータを参考にして予測します。
例えば、「今日の最高気温は35℃だったから、明日の外出は熱中症対策をしておこう」というのは、時系列近傍法の一例です。 ランダムウォークモデルと似た発想をしています。
また、例えば、「今日の最高気温は25℃だったが、最近１週間は、今日以外は30℃を超えていたから、明日の外出は熱中症対策をしておこう」というのも、時系列近傍法の一例です。移動平均モデルと似た発想をしています。
時系列近傍法は、全容がわかりにくい発展をしています。 以下にまとめてみました。
時系列近傍法では、予測できる部分と、できない部分に分けます。 予測できる部分は、その時点での平均値に当たるものです。 予測できない部分は、平均値からの距離の具体的な大きさです。
時系列分析の特徴は、「平均値」に相当するものが、時間的に変化していることなので、その変化を捉える方法が開発されて来ています。
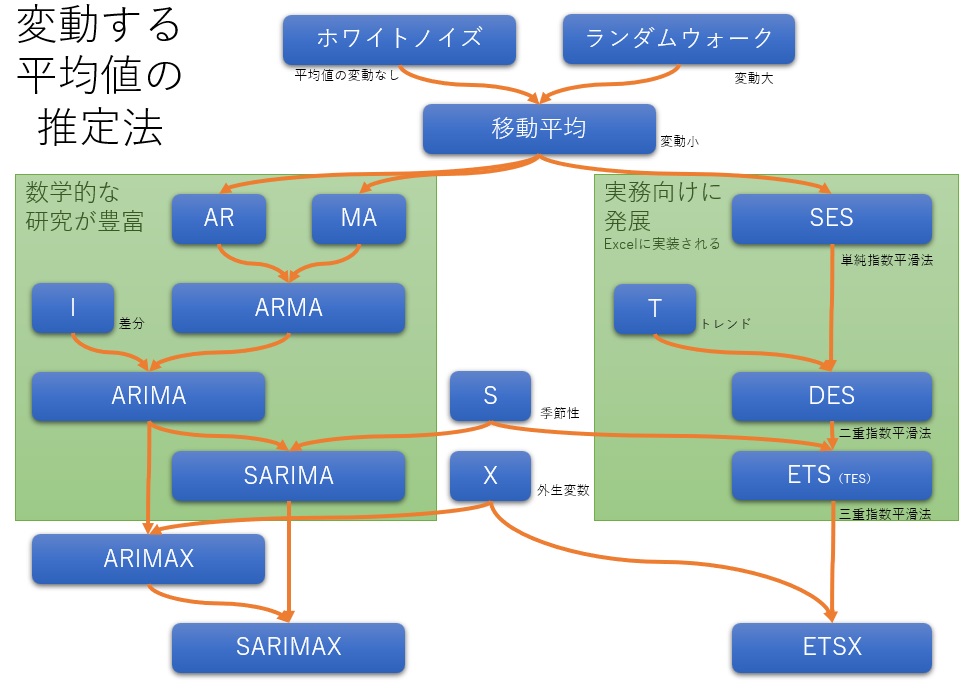
SARIMAXモデル の系統は、「無限個の場合」といったようにして、モデルの数学的な性質の研究が豊富なのも特徴です。
ETS（三重指数平滑法） の系統は、あまり知られていませんが、実用的です。 こちらの系統は、Excelで簡単に使えるようにもなっています。
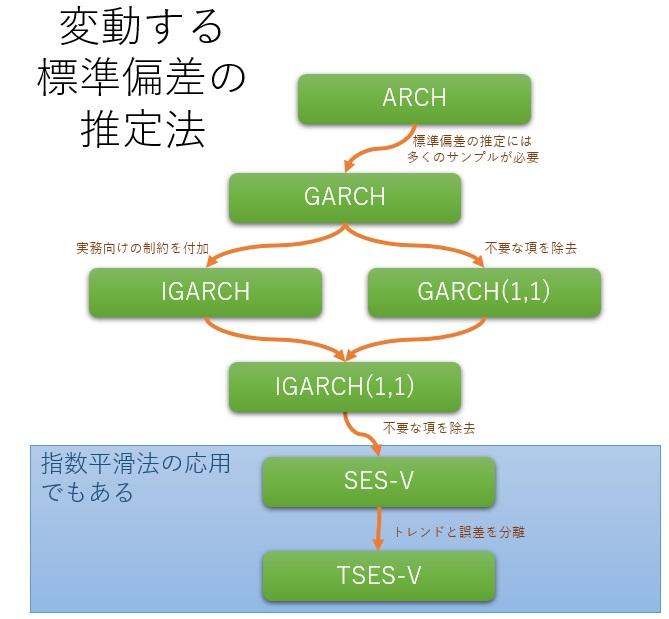
金融関係では、 ボラティリティ変動モデル として、標準偏差が変動する現象が研究されて来ています。
元々は、金融関係のものですが、作られたモデルは汎用的なので、「変動する標準偏差の推定法」として、他の分野でも活用できます。
時系列近傍法では、意識して、
X(n)
という書き方をしています。
時系列解析 なのに、それぞれのデータの添え字は、timeの「t」ではなく、「n」を使っています。
「n」は、「n番目の値」という意味です。
1時間おきに測定したデータなら、
「n番目 ＝ n時間後」
という意味になります。
ただ、それは特殊な場合です。
「n番目の値」というのが、どの場合にも当てはまる使い方になります。
時系列解析では、どうやって サンプリング されたデータなのかという メタ知識 が、とても重要な事があります。 大きく分けると、「1秒ごと」、「1時間ごと」、という風に均等な時間でサンプリングしている場合と、 「1回の生産ごと」、「トラブル発生ごと」、という風に均等でないことがあります。
どちらのケースでも、ソフトの中では同じように解析することができますが、 ソフト自体は「n番目」という風にしか扱っていない点が大事です。 解析結果を解釈したり、利用したりする場合の注意点になります。
扱っているのが「n」という点のもうひとつ大事な注意点が、 時系列近傍法では、ステップとステップの間で起きていることは、見ていない点です。 別の言い方をすれば、時系列近傍法は、離散データとして時系列の変化を見ていて、連続データとしては見ていません。
例えば、「１時間ごとの気温のデータ」でしたら、データとデータの間に特に変わった事は起きそうもないので、特に気にしなくて良さそうですが、 どういうものを、どういう風にサンプリングしたのかがわからないデータでは、重要な注意点になります。
離散データとして考えると、 ステップからステップへの変化は、数学的には「写像」という言葉で表現できます。
「何らかのルールに従って、あるステップの値を、次のステップの値に変換している。」と解釈してしまうと、 数学の写像の理論を使って、解析することができます。 このアイディアは、 カオス の研究で、さかんに使われています。
一般的に、タイトルで「時系列解析」を掲げている本は、 自己相関分析関係が多いです。 ちなみに、 「システム同定」というタイトルの本は、目的は システム同定 ですが、 「時系列解析」の本とほぼ同じ内容です。
自己相関分析は、伝統的に線形現象の知見が積まれています。 非線形現象については、 カオス の研究の知見によるところが大きいです。
「現場ですぐ使える時系列データ分析 データサイエンティストのための基礎知識」 横内大介・青木義充 著 技術評論社 2014
時系列データと、点過程データの違いの説明から始まります。
時系列データは、値の変化のデータです。折れ線グラフが一般的です。
一方、点過程データは、値の発生のタイミングと、その時の大きさを表します。
こちらは、横軸を時刻にした
棒グラフ
にします。
この本の場合は、データの種類の解説の後に、株のデータの分析を題材にしています。
自己相関分析が中心ですが、銘柄の関係の分析として、
クラスター分析
も出て来ます。
「時系列解析入門」 北川源四郎 著 岩波書店 2005
中級者向けかもしれませんが、線形の時系列解析について、よくまとまっている本です。
時系列データの自己相関分析から始まり、ARMAモデル、状態空間モデル、周波数解析等が解説されています。
時変係数ARモデル：係数も時間的に変動するモデル。ただし、変動は正規分布を仮定。
「情報の物理学」 豊田正 著 講談社 1997
統計力学と確率的な時系列解析について解説しています。
「確率と確率過程」 武田一哉 編著 オーム社 2010
自己相関係数の次に、相互相関係数が紹介されています。
相互相関係数は、自己相関係数と、一般的な相関係数の両方の特徴を持ったもので、時刻をずらして、異なる変数の相関を見るものです。
「時系列解析の方法」 尾崎統・北川源四郎 編 朝倉書店 1998
内容のほとんどは、線形現象です。
最小二乗法で求めたモデル式の係数は、必ずしも定常性を持たないので、
シミュレーションに使うと発散することがある。
ユール・ウォーカー法だと定常性を持つ。
ピリオドグラム解析 − 雑音がある中で、未知の周波数の強さを推定する方法
システム同定
、
カルマンフィルタ
、最適制御等の制御系の話が多めです。
フィードバックシステムは、入力と雑音に相関があるから、自己相関モデルが使えない。
ベイズモデルが、非定常時系列（季節変化、等）に使うモデルとして出て来ます。
非線形現象の予測や、構造の推定方法として、一般化ExpARモデルが紹介されています。
「非線形時系列解析」 松葉育雄 著 朝倉書店 2000
式の展開が比較的詳しいです。
「状態変数＝次元」ということで、次元の推定の話があります。
長期記憶性というのは、長時間前の状態の影響があることを言います。
長期記憶性の指標として、「ハースト数」が出て来ます。
「カオス時系列解析の基礎と応用」 合原一幸 編 産業図書 2000
[y(t),y(t+1)]のペアを散布図にすると、一見複雑に見えるデータのモデルが、簡単にわかることがある事を紹介しています。
わかるのは、yが写像になっている場合です。
「写像」という法則は、データの見方を工夫しないと、見つかりにくいことを指摘しています。
ちなみに、散布図が直線的な現象を表しているなら、
上記のように、自己相関分析ができます。この本は、もっと一般的な場合の話をしています。
ターケンスの埋め込み定理というのは、
「観測時系列から時間遅れ座標系へ変換」ということをするらしいです。
「カオスと時系列」 松本隆 他 著 培風館 2002
カオスを知る・発見する・予測する・事例研究という構成になっていて、カオスの本では変わっています。
ARモデル、線形確率過程のモデルが出て来ます。
「階層ベイズ的定式化」という、ニューラルネットワークそっくりのものが出て来ます。
「カオスを発見する」には、「次元の推定」が含まれます。
「理工基礎 確率とその応用」 逆瀬川浩孝 著 サイエンス社 2004
確率で使う道具を順に解説していて、
確率過程の入門があります。
順路
次は
時系列近傍法の基礎モデル
