自己相関モデル（ランダムウォークモデル）

このサイトには、ランダムウォークモデルのページがありますが、そこでは、シミュレーションのモデルとしてランダムウォークモデルを説明しています。

このページでは、時系列近傍法の基礎として、ランダムウォークモデルを説明します。

時系列近傍法としてのランダムウォークモデルは、 ARMAモデルの一番シンプルな形でもあります。

ランダムウォークモデルによる予測

下のグラフは、とても複雑な動きをしている時系列データです。
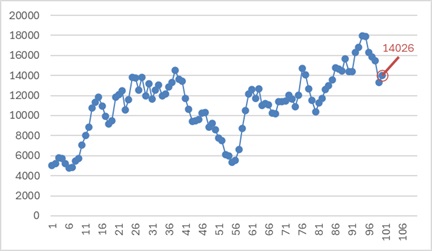
ランダムウォークモデル

一番新しいデータは、「14026」となっていますが、次のデータはいくつと予測したら良いでしょうか？

ホワイトノイズモデルの場合は、全部のデータの平均値を予測値にしていますが、この例の場合は、もっと精度の高い予測ができます。

それは、「14026」です。一番新しいデータを、予測値の中心値と考えます。

ホワイトノイズモデルでは、隣接するデータとは、まったく似ていない値になっていましたが、上の例では、隣接するデータとは似ています。それを根拠にすると、一番新しいデータを予測値にできます。

ランダムウォークモデルの場合も、予測値は、中心値だけでなく範囲で把握できた方が実用的な予測になります。

予測値に全体の平均値を使わなかったように、範囲も全体の標準偏差は使わない方が、精度が高いです。

この例では、だいたい同じくらいの長さで、値が変化しているので、 RMSE が使えます。

ランダムウォークモデルでは、予測値を前のデータとするので、誤差は、前のデータとの差です。その差で、RMSEを計算します。

ランダムウォークモデルは、１ステップ前の値に、乱数が足し合わさることで、次の値が決まるモデルです。

式は、以下のようになります。
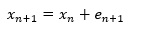
ランダムウォークモデル

ホワイトノイズモデルで、一定値を表すuのところが、n番目のxに置き換わっています。

ランダムウォークモデルが当てはまるデータでは、隣接するサンプルと値が近いです。これを「自己相関」と言います。自己相関分析に応用できます。

株価は、ある時の値に、足したり引いたりして、次の時の値が決まるので、ランダムウォークモデルが、モデル式になります。

株価のモデルとして、ランダムウォークモデルを使う時には、そうしたもっともらしさがあります。

一方、実際にデータができる仕組みとは無関係に、「隣接するサンプルは、値が近い」というデータの特徴だけから、予測モデルを作る時は、事情が異なります。他の予測モデルとは異なるところがあります。

統計的な予測モデルでは、平均的や、もっとも確率が高い値を予測値の中心値にします。そうした中心値を、何らかのモデルを仮定して計算します。

ランダムウォークモデルでは、計算をせず、１ステップ前のデータ自体を、予測値の中心値にする点が異なります。

ランダムウォークモデルでは、差分が誤差になりますが、これはランダムウォークモデルの特異性があるためです。他のモデルでは、こんなに簡単に誤差は求まりません。