・・・①で表現できます。 X の１乗の項のみなので、「X の一次式」と言います。 B が０の時、直線は原点を通ります。
相関性 の解析のように、データが直線状に並ぶかどうかを評価することは、 データサイエンス では、よくされています。
直線を表す数式は、
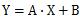・・・①
で表現できます。
X の１乗の項のみなので、「X の一次式」と言います。
B が０の時、直線は原点を通ります。
X が n 個ある時は、
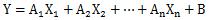・・・②
と表現できますが、これを「線形和」と言います。
線形和は、X の一次式の和（足し算）です。
①や②の式を「線形式」と言います。
この式で表現できる現象は、
「線形性（Linearity）がある。」という言い方をします。
式①は「直線」を表す式です。
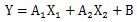
は、「平面」を表す式です。
そして、式②のように、
X が３個以上ある場合は、「超平面」を表す式です。
「超平面」は、グラフに描けません。
①や②の式は、 回帰分析 でも登場する式です。
①の式を求めるための回帰分析は、「線形単回帰分析」と言います。 ②の式を求める時は、「線形重回帰分析」です。
線形式をモデル式として仮定することを、「線形近似」と言います。 下記のような４つの理由があり、 データサイエンス では、線形近似がよく使われます。
線形式は、式が単純なこともあり、 相関係数 等の多彩な理論が作られています。 線形近似が可能となれば、様々な観点から調べられるようになります。
線形式は、わかりやすいです。 一度は、試したくなる魅力を持っています。
正規分布 を仮定することに無理がありそうな分布にも正規分布を仮定して（近似して）、 それなりに使える成果を出せることがあります。 これは、正規分布の理論がロバスト（頑健）だからです。 この点で、線形近似の理論は、正規分布の理論と似ています。 線形近似の理論もロバストです。
グラフで見ると、直線にはなっていなくても、グラフの増加や減少の傾向がある場合であれば、 線形と考えても、それなりに当てはまります。
例えば、Yの増減と関係しているXの候補として、とりあえず増加や減少のあるXを抽出したい時には、 線形近似の理論が役に立つこともあります。
数学には、現象を数式で表す時に、簡単な数式から組み立てて、だんだん難しい数式を足し合わせていくアイディアがあります。 「テイラー展開」、等と呼ばれています。
このアイディアを使うと、「極微小な範囲の変化は、線形式で表せる。」と言えます。 つまり、極微小な範囲の解析では、線形近似で十分という意味です。
「大きい」、「小さい」というのは、相対的なものなので、 日常的な状況や、外乱のないような理想的な状況では、「極微小」の範囲に入ってしまうことがあります。 古典的な物理学や化学では、このような現象を「法則」として見つけて来ています。
線形でないのが、非線形です。 自然現象は、一般的に非線形です。 線形が直線で表せるような現象なので、 非線形は曲線（カーブ）で表せるような現象だと考えることもありますが、 曲線は、非線形の世界の一部でしかありません。 カオス は、非線形のひとつの極みです。
曲線なら、線形の解析の延長で扱えることもありますが、 一般的には、非線形の解析は、技があまりありません。
数学的なアプローチでデータを解析する方法として、線形近似は強力です。 しかし、現実世界のデータでは、線形近似がうまくいかないことが、よくあります。
筆者の経験の範囲では、 線形近似で解析をしても何も成果がない場合や、 「極微小」の範囲とは考えられない場合等の時には、 非線形の数学で何とかしようとしても、良い結果は出ないです。 モデル式で現象を表現しようとすることに無理があります。
それよりも、 「とにかくグラフを良く見る」、「データの背景を調べる」、「現象の背景を調べる」等の、 数学以外のアプローチが、現実的な突破口になることの方が多いです。
順路
次は
標準偏回帰係数
