 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
データを直接 重回帰分析 するのではなく、変数ごとに 標準化 してから 重回帰分析 した場合の偏回帰係数は、「標準偏回帰係数」と呼ばれます。
説明変数が、「身長と体重」など、単位が異なる場合、これらを使った重回帰分析のモデルでは、偏回帰係数の単位が異なります。 そのため、偏回帰係数同士を比較することができません。
データを標準化しておくと、無次元になるため、偏回帰係数同士の比較ができるようになります。
説明変数同士が独立して考えることができるのなら、標準偏回帰係数の絶対値が大きな変数ほど、目的変数に影響の大きな変数と考えることができるようになります。
説明変数同士が独立しているのなら、標準偏回帰係数は、各変数と目的変数の 相関係数 です。 この性質は、 傾きと相関係数と標準化 の話と、同じです。
また、標準偏回帰係数の2乗は、目的変数に対しての 個別の因子の寄与率 になっています。
個別の因子の寄与率 のページにあるように、実際のデータでは「説明変数同士が独立している」ということは、あまりないのですが、 「説明変数同士が独立している」に近い状況なら、この知識は役に立ちます。
Y、X1、X2という3個の変数について、「Y = A1 * X1 + A2 * X2 + B」という重回帰分析を考えます。
A1とA2が、偏回帰係数です。
A1を求める式は、以下になります。Sというのは、平方和です。この式の求め方の説明は、省略します。
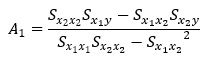
標準化されていると、上記の式のSの部分を、S'に入れ替えるのですが、S'と相関係数rには、以下の関係があります。
tというのは、標準偏差です。
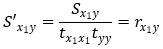
上記の平方和Sの部分が、相関係数rに置き換わります。
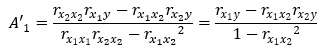
つまり、以下のようになります。標準偏回帰係数は、3つの相関係数でできています。
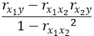
順路


 次は
変数の重要度の分析
次は
変数の重要度の分析

